http://dx.doi.org/10.5762/KAIS.2013.14.1.1
Journal of the Korea Academia-Industrial cooperation Society Vol. 14, No. 1 pp. 1-6, 2013
이준성 1* 1 경기대학교 기계시스템공학과
Integrity Evaluation for 3D Cracked Structures(II)
1 Dept. of Mechanical System Engineering, Kyonggi University
요 약 3 차원 균열은 항공기나 압력용기 계통에서 흔히 발견되는 결함중의 하나이다 . 균열을 갖는 구조물에 대한 정확한 응력확대계수 해석과 균열성장속도는 파괴강도와 피로수명을 평가하는데 필요로 한다 . 3 차원 유한요소법은 구 조물에 존재하는 표면균열의 응력확대계수를 구하는데 이용되어 진다 . 기하모델 , 즉 균열을 포함하는 솔리드모델을 정의한 후 , 절점이 버켓법에 의해 생성되어 진다 . 요소생성은 사변형 솔리드요소를 데라우니 삼각화 기술에 의해 생 성하도록 하였다 . 시스템의 정확도와 효용성을 체크하기 위해 내압을 받는 원통형용기에 균열이 존재하는 경우의 응 력확대계수 해석을 수행하였다 . 개발된 시스템을 이용한 해석결과는 ASME 식과 Raju-Newnam 식과 비교하여 5% 이내 의 차이를 보였다 .
Abstract Three Surface cracks are among the more common flaws in aircraft and pressure vessel components.
Key Words : Surface Crack, Stress Intensity Factor, Finite Element Analysis, Mesh Generation
3차원 균열을 갖는 구조물에 대한 건전성 평가(II)
Joon-Seong Lee1*
Abstract
Accurate stress intensity analyses and crack growth rate data of surface-cracked components are needed for reliable prediction of their fatigue life and fracture strengths. Three Dimensional finite element method (FEM) was used to obtain the stress intensity factor for surface cracks existing in structures. A geometry model, i.e. a solid containing one or several 3D cracks is defined. Nodes are generated by bucket method, and quadratic tetrahedral solid elements are generated by the Delaunay triangulation techniques. To examine accuracy and efficiency of the present system, the stress intensity factor for a semi-elliptical surface crack in cylindrical structures subjected to pressure is calculated. Analysis results by present system showed good agreement with those by ASME equation and Raju-Newman’s equation.
1. 서론 원자력발전소의 주요기기는 고온 고압의 가동조건하 에서 안전성을 유지할 수 있도록 ASME Boilier and Pressure Vessel Code Section III [1]에 준하여 설계한다. 이렇게 설계된 원자력발전소 주요기기에는 재질의 불균 일성이나 용접과정상의 문제 등의 이유로 미소균열이 존 재할 수 있으며 이러한 미소균열 중 일부는 가동 시 계속 적인 반복하중을 받음으로써 기기 건전성에 영향을 미칠
수 있는 크기의 균열로 성장할 수도 있다. 가동 중인 원 자력발전소에서 이러한 결함이 발견될 경우, ASME Section XI[2]에 준한 결함 안전성 평가를 수행하여 그 안 전성이 입증되어야만 계속 가동할 수 있다. 국내의 중수형 원자로는 핵연료의 교체가 용이하게 원 자로를 수평으로 설치하고 여기에 중수형 원자로 압력관 을 설치한다. 압력관은 고온 고압의 가동환경에서 균열발 생 확률이 높으며 나중에는 균열이 진전하여 압력관의 파손을 유발한다[3]. 압력관 결함의 건전성 평가를 위해
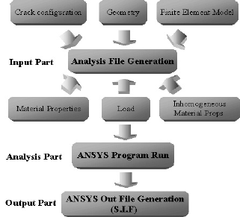
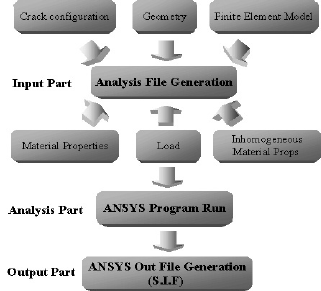
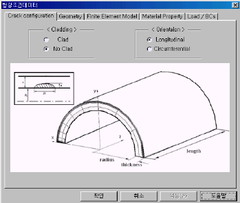
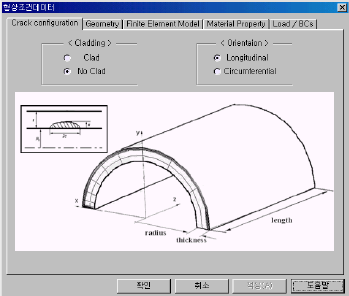
본 연구에서 개발한 시스템의 주요 입력파라미터는 Table 1에 나타내었으며, 단위는 SI, USCS 모두 사용가 능하도록 하였다. Fig. 1은 시스템의 전체적인 구성을 나 타낸 것이다. 입력부의 하나의 예로서 Fig. 2는 원통형 용 기에 균열이 존재하는 경우, 균열의 방향이 축방향인지 원주방향인지를 선택하고 구조물에 클래드(clad)가 있는 지 없는지를 선택하는 입력창을 나타낸 것이다.재료물성 치인 탄성계수 E, 포아송의 비 ν, 그리고 간단한 이름을 입력받는다. 클래드가 있는 경우는 클래드에 대한 E, ν도
[Fig. 2] Example of input screen of crack shape
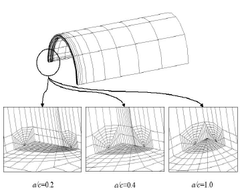
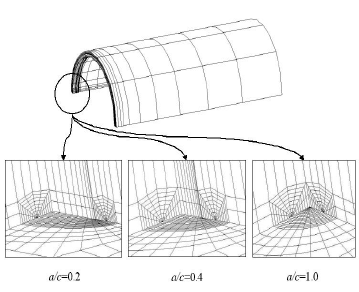
입법을 제안하고자 한다. 구체적으로는 구조물의 형상을 정의할 때, 균열을 넣고 싶은 위치에 타원체를 도려냄으 로써 균열부의 상하면을 연결하지 않도록 하면 된다. 요 소가 생성된 후, Fig. 3에서 보는 바와 같이 절점좌표를 z방향으로 이동한 타원체를 찌부러뜨리는 것에 의해 균 열부의 표현을 실현 가능케 하여준다. 여기서 r x 는 균열 의 장반경, r y 는 균열의 깊이, r z 는 타원체의 z방향으로의 반경이다. 또한, 2.1항에서 입력한 타원체로부터 타원을 생성할 때 필요한 h는 절점을 이동하는 범위를 나타내는 파라미터이다. 사용자는 솔리드모델러를 이용하여 형상
여기서 2c : 결함길이 a/2c : 결함비 q y : 소성역 보정계수 이다. 이때 소성역 보정계수는 식 (4)와 같다.
References
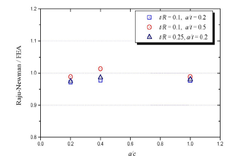
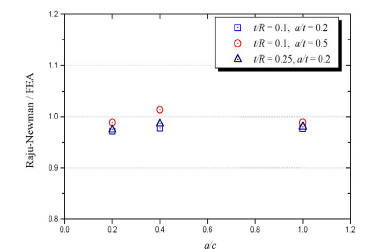
- [Fig. 6] Comparison of stress intensity factor between Raju-Newman and FEA
Thickness Variation,” Fitness for Service Evaluation and Non-Linear Analysis, Proceedings of the ASME Pressure Vessels and Piping Conference, PVP Vol. 442, pp. 111-118, 2006. [4] Y.J. Choi, J.S. Lee, Y.J. Yoo, “Fracture Analysis for Ceramic Disk with Semi-Elliptical Crack and Pore”, Proceedings of KSPE 2012 Spring Conference, pp. 957-958, 2012. [5] J.S. Lee, “Automated CAE System for Three-Dimensional Complex Geometry”, Doctoral Thesis, The University of
• 1988년 2월 : 성균관대학교 대학 원 기계공학과 (공학석사) • 1995년 9월 : 동경대학교 (공학 박사) • 1988년 7월 ~ 1991년 7월 : 육 군사관학교 교수부 기계공학과 교수 • 1996년 3월 ~ 현재 : 경기대학 교 기계시스템공학과 교수 <관심분야> 최적설계, Neural Network, 구조물 수명평가