한국산학기술학회논문지 Vol. 11, No. 7 pp. 2328-2333, 2010
* 교신저자 : 김국현(kimk@tu.ac.kr) 접수일 10년 04월 26일 수정일 (1차 10년 06월 16일, 2차 10년 06월 23일)
게재확정일 10년 07월 06일
2328
음향방사문제에서 직접경계요소법의 비유일성 회피방법에 관한 고찰
구성되는 내부 공간에 대한 가상의 고유진동특성에 따라 홀쯔 적분방정식(Helmholtz integral equation)으로부터 계 정확한 해를 얻을 수 없게 된다. 이러한 문제를 해결하기 산할 수 있다[7].
간 상 수신기 위치 에서의 음압은 식 (1)과 같은 헬름
분식에 적용하고 각각의 절점에 대한 음압 과 속도
2329
한국산학기술학회논문지 제11권 제7호, 2010
(7)
을 이용해 좌표계로 변환하여 정리하면, 식 (4) 및 식 (5)와 같은 행렬식을 얻을 수 있다.
이용해 수음점 에서의 음압
며, 최종적으로 식 을 계산할 수 있다.
하지 않으며, 식 (8)의 영향행렬이 정방행렬(square matrix)로 나타나지 않는 등의 단점이 있다.
2330
음향방사문제에서 직접경계요소법의 비유일성 회피방법에 관한 고찰
3. 수치해석 및 고찰
2.2.2 ICA-Ring 방법 ICA-Ring 방법은 경계면을 일정한 두께를 갖는 쉘
2331
한국산학기술학회논문지 제11권 제7호, 2010
4. 결론
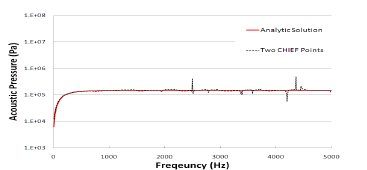
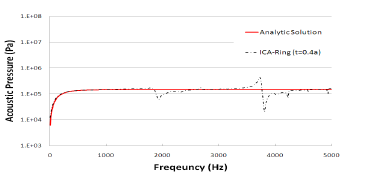
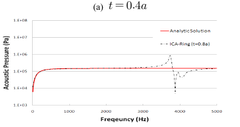
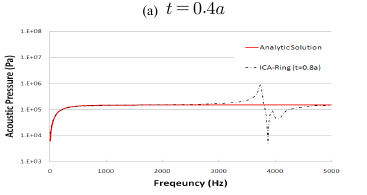
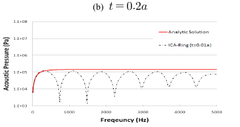
[그림 6] ICA-Ring 방법에 의한 해의 비유일성 회피결과
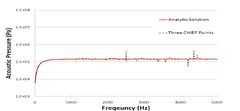
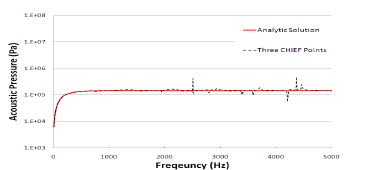
(c) CHIEF 점 개수: 3 [그림 5] CHIEF 방법에 의한 해의 비유일성 회피결과
2332
음향방사문제에서 직접경계요소법의 비유일성 회피방법에 관한 고찰
[표 2] 쉘의 두께 적용에 따른 주파수구간별 오차 Freq.
김 국 현
음향방사문제에서 직접경계요소법의 비유일성 회피방법에 관한 고찰
Kookhyun Kim1*
Abstract
A direct boundary element method(DBEM) is widely applied for various acoustic wave problems. But this method has numerically non-unique solutions around the eigenfrequencies of the interior Dirichlet problem for the region enveloped with the acoustic boundary. A CHIEF method had been generally adopted to resolve the non-uniqueness problem and a new technique called ICA-Ring method has been suggested recently. In this paper, the characteristics of two techniques for avoiding the non-uniqueness of DBEM are examined and numerical codes embodying both techniques are developed. Numerical calculations are also carried out for an uniformly pulsating sphere, of which the results are investigated by including the comparisons with theoretical solutions. Key Words : Exterior Acoustic Wave Radiation Problem, Direct Boundary Element Method, Non-uniqueness Problem, CHIEF Method, ICA-Ring Method
김국현 1* 1 동명대학교 조선공학과 Investigation on Method Avoiding Non-uniqueness of Direct Boundary Element Method in Acoustic Wave Radiation Problem
1 Department of Naval Architecture, Tongmyong University 요 약 직접경계요소법은 음향방사문제 해석에 널리 적용되는 수치해석기법중 하나이지만 , 외부 음향방사 문제에 있 어서는 방사면 내부공간의 고유주파수 근방에서 비유일성이 나타나게 된다 . 이를 해결하기 위한 방법으로 CHIEF 방 법이 일반적으로 적용되어 왔으며 , 최근 들어서는 ICA-Ring 방법과 같은 새로운 기법이 제안되어 해의 정확도 향상 에 기여하고 있다 . 본 논문에서는 앞서 언급한 두 가지 비유일성 회피기법들의 특성을 살피고 , 각각의 기법 구현을 포함한 직접경계요소법 기반의 수치해석 코드를 작성한다 . 또한 , 법선방향 균일속도로 진동하는 구의 음향방사문제에 대한 수치해석을 수행하고 그 결과를 해석 해와 비교하여 각각의 기법들에 대한 비유일성 회피 성능을 고찰한다 .
1. 서론 경계요소법 (boundary element method)은 유한요소법 (finite element method)과 함께 음향문제 해석을 위해 가 장 효과적으로 널리 사용되고 있는 수치해석방법이다[1]. 뿐만 아니라, 경계요소법은 유한요소법과 같이 음장공간 전체를 3차원 요소로 이산화(discretizing)하지 않고 경계 면만을 2차원 요소로 이산화하여 음향 산란(scattering)/방 사(radiation) 문제와 같이 음장공간이 무한영역으로 되어 있는 경우에 더욱 효과적으로 적용될 수 있다.
경계요소법은 헬름홀쯔 적분방정식 (Helmholtz integral equation)에 대한 수치해를 구하는 방법이며, 정 식화 과정에 따라 직접경계요소법 (direct boundary element method)[2]과 간접경계요소법(indirect boundary element method)[3]으로 분류된다. 특히, 직접경계요소법 은 간접경계요소법에 비해 정식화가 간단하고 유한요소 법과 행렬 결합이 용이해 유체와 구조가 연성된 음향 산 란 및 방사문제에 대해서도 효과적으로 적용되고 있다 [4]. 그럼에도 불구하고 직접경계요소법은 무한 공간에 대한 음향산란 또는 방사문제를 해석할 때 경계면으로
위해 CHIEF(combined helmholtz integral equation formulation) 방법이 주로 적용되어 왔다. CHIEF 방법이 란 CHIEF 점이라 불리는 가상의 음원들을 경계면 내부 영역에 분포시켜 overdetermined 행렬을 구성하고 해를 구하는 방법을 말한다. 그러나 CHIEF방법은 최적의 가 상 음원 수와 분포 위치를 결정하기가 쉽지 않아 대부분 의 연구자들의 경험에 의존하는 실정이다. 한편, and Fujiwara[6]는 경계면을 얇은 쉘(shell)로 가정하여 비 유일성을 해결하는 새로운 방법을 제안하고 전형적인 음 파 산란문제 중 하나인 2차원 방음벽의 삽입손실 (insertion loss) 해석에 응용한 바 있다. 또한, Hirosawa 등[7]은 Ishizuka and Fujiwara이 제안한 비유일성 회피방 법을 ICA-Ring 방법(inner cavity ringing method)으로 명 명하고 보다 수학적이고 체계적으로 정식화하였으며, 2 차원 다중영역(plural domain) 산란문제로 확장한 바 있 다. 본 연구에서는 앞서 언급한 법 등의 비유일성 음향방사문제에 확장/적용하고 각각의 방법들에 대한 특징과 성능을 고 찰하고자 한다. 이를 위해 각각의 비유일성 회피방법을 고려한 직접경계요소법을 정식화하고 이를 바탕으로 수 치해석 코드를 작성한다. 또한, 법선방향 균일 속도로 진 동하는 구(sphere)의 음향방사문제에 대한 수치해석을 수 행하고 그 결과를 해석 해와 비교하여 각각의 기법들에 대한 비유일성 회피 성능을 고찰한다.
2. 직접경계요소법 직접경계요소법은 음향방사문제에 있어서 효과적인 수치해석방법중 하나이지만, 특정 주파수 근방에서 정확 한 해를 구할 수 없는 단점이 있다. 이는 경계면 내부음 장에 대한 Dirichlet 경계조건에서의 고유주파수 (eigen-frequency)에 해당하는 주파수 근방에서 발생하는 해의 비유일성(non- uniqueness) 때문이다. 본 장에서는 수치해석 코드 작성을 위한 직접경계요소법을 정식화 하 고 CHIEF 방법, ICA-Ring 방법 등의 비유일성 회피방법 에 대해 정리한다. 2.1 직접경계요소법 그림 1에 보인 바와 같이 진동하는 경계면에 의한 공
Ishizuka
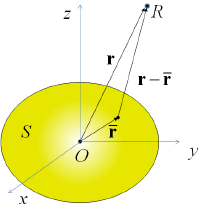
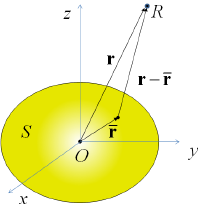
[그림 1] 음향방사문제 좌표 정의 (1)
ICA-Ring방
CHIEF 방법, 회피방법들을 3차원
여기서, 과 는 각각 수신기 위치벡터 과 경 계면상 임의 위치벡터 에서의 음압, 은 경계면의 법선 에 대한 편미분, 는 경계면, 는 체적각도(volume angle)로서 수신기가 부드러운 경계면상에 있는 경우 1/2, 자유공간에서는 1의 값을 갖는다. 또한, 는 식 (2) 로 정의되는 자유음장 그린함수(Green function)이다. (2) 여기서, , 는 파수를 의미한다. 한편, 그림 1에 나타낸 경계면 를 유한개의 평면요소 로 근사화하고 = 의 관계식을 식 (1)에 대입하여 정리하면 식 (3)을 얻을 수 있다. (3) 여기서, 는 음장공간의 유체밀도, 는 각주파수, 는 에서의 경계면의 법선방향 속도, 은 경계면 의 평면분할 수, 는 번째 평면을 의미한다. 분할된 경계면 에 대해 4-절점 선형요소(4-node linear element)[8]를 식 (3)의 우변 첫 번째와 두 번째 적
(4) (5) 여기서, 또한, 식 (4)와 식 (5)를 이용해 식 (3)을 전체 절점에 대한 행렬방정식으로 나타내면 식 (6)이 된다. (6) 여기서, 와 는 크기가 × 인 영향행렬, 은 총 절점 수를 의미하며, ⋯ ⋯ ⋮⋱ ⋮⋱ ⋱⋮ ⋱⋮ ⋯ ⋯ ⋯ ⋯ , ⋯ ⋯ .
이와 같이 식 (6)을 이용해 경계면상의 모든 절점에서 의 속도벡터 로부터 음압벡터 를 계산할 수 있으 (7)을
2.2 비유일성 회피방법 앞서 언급한 바와 같이 직접경계요소법을 이용해 음향 방사문제를 해석하기 위해서는 경계면 내부공간의 Dirichlet 경계문제에 대한 고유주파수 근방에서 발생하 는 해의 비유일성을 회피하여야 한다. 2.2.1 CHIEF 방법 현재 해의 비유일성을 회피하기 위한 방법으로 CHIEF 방법이 가장 널리 사용되고 있다. CHIEF 방법이란 경계 면 내부영역에 CHIEF 점이라고 불리는 가상의 음원들을 배치하여 식 (6)에서 영향행렬 와 의 조건수 (condition number)를 낮춰 해의 안정성을 높임으로써 해 의 비유일성을 회피하는 방법이다. 식 (8)은 CHIEF 점들 을 배치할 경우에 대해 식 (6)을 수정한 결과이다. (8) 여기서, 와 는 CHIEF 점들에 따른 추가행렬 이며, 그 크기는 CHIEF 점들 개수가 일 때 × 이다.
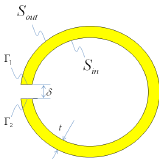
[그림 2] ICA-Ring 방법의 개념
[그림 3] 구에 대한 경계요소 모델 ( 요소수 =384) CHIEF 방법은 Schenck[5]가 처음으로 제안한 이후로 많은 연구자들에 의해 개선이 이루어져 왔음에도 불구하 고 CHIEF 점들에 대한 최적 위치와 개수를 선정이 용이
(shell)로 가정하고 바깥쪽 경계면과 안쪽 경계면을 동시 에 모델링하여 해의 비 유일성을 회피하는 방법이다. 그 림 2는 ICA-Ring 방법을 개념적으로 설명하기 위해 3차 원 문제를 2차원 문제로 단순화 하여 나타낸 것이다. 경계면 가 바깥면 과 안쪽면 , 바깥쪽과 안쪽 면을 연결하는 크기가 인 구멍에 의해 형성되는 미소면 와 로 구성된다고 가정하면 식 (1)의 우변은 식 (9)와 같이 다시 쓸 수 있다. (9) 또한, lim → 이므로 식 (9)는 식 (10)이 된다. (10) 즉, 식 (1)의 경계면 에 대한 적분방정식은 식 (10)과 같이 바깥경계면 과 내부 경계면 각각에 대한 적 분방정식의 합이 된다. ICA-Ring 방법은 CHIEF방법과 달리 별도의 정식화 과정이 필요하지 않고 단지 경계면 으로부터 일정 두께 만큼 떨어진 가상의 내부 경계면을 추가함으로써 해의 비유일성을 해결할 수 있는 방법이다. 한편, Hirosawa 등[7]은 ICA-Ring 방법을 적용할 경우, 쉘의 두께를 작게 모델링할수록 비유일성이 나타나는 주 파수가 높아지는 특성을 2차원 원통형상 산란문제에 대 한 수치해석을 통해 보인 바 있다.
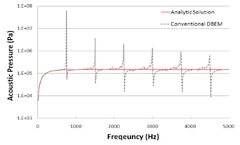
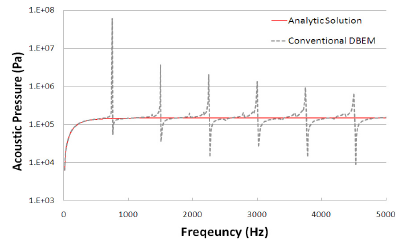
직접경계요소법의 비유일성을 회피하기 위해 일반적 으로 적용되고 있는 CHIEF 방법과 최근 새롭게 제안된 ICA-Ring 방법의 특성과 성능을 고찰하고자 법선방향 균 일속도(1 )로 진동하는 구의 음향방사문제에 대한 수치해석을 수행하였다. 그림 3은 수치해석모델을 보인 것으로 반지름 는 1m이며, 384개의 4-절점 선형요소 모 델링하였다. 이 때, 수신기의 위치는 모델 중심으로부터 10m 떨어져 있으며, 음향공간의 유체밀도는 1000 , 음속은 1500 , 해석 주파수는 10Hz에서 5000Hz까지 10Hz 간격이다. 그림 4는 기존 직접경계소요법을 이용한 수치해석결 과(conventional DBEM)를 해석해(analytic solution)[4]와 함께 도시한 것으로 특정 주파수에서 규칙적으로 해의 비유일성이 나타나고 있다.
[그림 4] 기존 직접경계소요법을 이용한 수치해석결과와 해석해 비교 [표 1] CHIEF POINT 수에 따른 주파수구간별 오차 Freq. Range(Hz) CHIEF Point Number from to 0 1 2 3 10 1000 504.9% 1.8% 1.6% 1.8% 1010 2000 34.4% 3.2% 3.0% 4.8% 2010 3000 42.1% 6.3% 3.5% 6.7% 3010 4000 29.9% 5.5% 3.3% 8.5% 4010 5000 20.9% 12.9% 3.8% 10.5% 그림 5는 CHIEF 방법에 의한 비유일성 회피 결과를 해석해와 함께 보인 것이며 표 1은 주파수 구간별 오차율 을 식 (11)에 따라 정리한 것이며, CHIEF 점 1개 추가 하였을 때 해의 비유일성이 완화되어 오차가 상당한 수 준으로 줄어들었으나 CHIEF 점의 수를 증가에 따른 효 과가 그리 크지 않음을 알 수 있다.
여기서, 와 은 해석해와 수치해석결과를 의미하 며, 과 는 오차분석 주파수 구간의 하한과 상한을 나 타낸다. 한편, 쉘의 두께 를 0.5 , 0.4 , 0.3 , 0.2 , 0.1 , 0.01a로 줄여가면서 ICA-Ring 방법으로 수치해석을 수행 하였다. 그림 6은 , , 에 대한 결과만을 해석해와 함께 나타낸 것이며, 표 2는 식 (11)을 이용해 쉘의 두께 증가에 따른 주파수 구간별 오차분석 결과를 정리한 것이다. Hirosawa 등[7]의 결과와 같이 전 반적으로 쉘의 두께가 작아질수록 해의 비유일성 회피성 능이 향상되고 있음을 알 수 있다. 반면, 쉘의 두께가 0.01 인 경우에는 해의 정확도가 오히려 상당 수준 떨어 지고 있음을 관찰할 수 있다. 따라서 ICA-ring 방법을 이 용해 정도 높은 해석을 수행하기 위해서는 적절한 수준 의 쉘 두께 설정이 필요할 것으로 판단된다.
(a) CHIEF 점 개수: 1
(b) CHIEF 점 개수: 2
본 논문에서는 3차원 음향방사문제에 직접경계요소법 적용할 때 나타나는 해의 비유일성에 대한 회피방법에 대해 고찰하였다. 이를 위해 CHIEF 방법, ICA-Ring방법 등의 비유일성 회피방법을 고려한 직접경계요소법을 정 식화하였으며, 이를 기반으로 수치해석 코드를 작성하였 다. 또한, 법선방향 균일 속도로 진동하는 구에 대한 수치 해석 수행을 통해 각각의 비유일성 회피방법에 따른 성 능을 살펴보았다. CHIEF 방법의 경우, CHIEF 점 1개 추 가하였을 때 해의 비유일성이 상당히 줄어들었으나 CHIEF 점의 수를 증가시키더라도 큰 효과가 없음을 알 수 있었다. 따라서 적절한 CHIEF 점의 개수와 위치 설정 이 필요할 것으로 사료된다. ICA-Ring방법의 경우, 쉘의 두께를 작게 설정할수록 해의 정확도가 향상되었으나 쉘 의 두께를 과도하게 작게 설정할 경우 오히려 해의 정확 도가 저하될 수 있으므로 경계면을 구성하는 요소 크기 를 고려해 쉘의 두께를 적절히 선정해야 함을 알 수 있었 다.
(c)
Shell Thickness, t Range(Hz) from to 0.5a 0.4a 0.3a 0.2a 0.1a 0.01a 10 1000 0.4% 0.5% 0.8% 2.9% 4.4% 45.0% 1010 2000 13.7% 11.8% 4.0% 0.7% 4.7% 49.6% 2010 3000 16.9% 10.4% 29.4% 6.5% 6.6% 61.3% 3010 4000 18.4% 34.4% 7.6% 73.7% 4.1% 55.9% 4010 5000 37.2% 11.9% 28.2% 24.2% 0.9% 56.7% 참고문헌
- [1] M. J. Crocker, “Handbook of Noise and Vibration Control”, John Wiley & Sons, Inc. 2007.
- [2] K. -D. Ih and D. -J. Lee, "Development of the Direct Boundary Element Method for Thin Bodies with General Boundary Conditions", Journal of Sound and Vibration, Vol. 202, No. 3, pp. 361-373, 1997.
- [3] Z. Zhang, N. Vlahopoulos, S. T. Raveendra, "Formulation of a Numerical Process for Acoustic Impedance Sensitivity Analysis based on the Indirect Boundary Element Method", Engineering Analysis with Boundary Elements, Vol. 27, No. 7, pp. 671-681, 2003
- [4] F. Holmström, "Structure-acoustic Analysis Using BEM/FEM; Implementation in MATLAB", Master's Dissertation, Lund University, 2001.
- [5] H. A. Schenck, "Improved Integral Formulation for Acoustic Radiation Problems", Journal of Acoustical Society of America. Vol. 44, pp. 41-58, 1968.
- [6] T. Ishizuka and K. Fujiwara, "Performance of Noise Barriers with Various Edge Shapes and Acoustical Conditions", Applied Acoustics Vol. 65, pp. 125-141, 2004.
- [7] K. Hirosawa, T. Ishizuka, and K. Fujiwara, "A Simple Method Avioding Non-uniqueness in the Boundary Element Method for Acoustic Scattering Problem", Journal of Acoustical Society of America. Vol. 125, No. 5, pp. 2838-2846, 2009.
- [8] K. Bathe, “Finite Element Procedures”, Prentice- Hall International Inc., 1996.
- (Kookhyun Kim) [정회원] • 1996년 2월 : 인하대학교 일반대 학원 선박공학과 (공학석사) • 2007년 2월 : 부산대학교 일반대 학원 조선해양공학과 (공학박사) • 1996년 8월 ~ 2009년 8월 : (주) 한진중공업 책임설계원 • 2009년 9월 ~ 현재 : 동명대학교 조선공학과 전임강사
- <관심분야> 구조/진동/소음, 스텔스(RCS, URN)