FSM을 이용한 수정된 유클리드 알고리즘 설계

강성진 1*

A Design of Modified Euclidean Algorithm using Finite State Machine Sung-Jin Kang 1*

요 약 본 논문에서는 FSM(finite-state machine) 을 이용하여 차수 계산 (degree computation) 을 하지 않고 수정된 유클 리드 알고리즘 (modified Euclidean algorithm) 을 구현할 수 있는 구조를 제안한다 . 제안된 구조는 차수계산이 필요없기 때문에 RS(Reed-Solomon) 복호기의 하드웨어 복잡도를 줄일 수 있고 , 고속의 복호기 설계가 가능하게 된다 . 제안된 구조를 이용하는 RS(255,239) 복호기를 Verilog HDL 로 구현하였고 , 기존의 복호기에 비해 게이트 수를 약 13% 정도 줄일 수 있다 .

1. 서론

RS 부호는 연집 오류에 대하여 우수한 오류 정정 능력을 가지고 있어서, 광/자기 저장매체, 유무선 통신, 방송, 위성 통 신 등 많은 통신시스템에서 널리 사용되고 있다. 또한, 최근 에는 플래시 메모리 분야에서도 오류 정정을 하기위 한 연구가 활발히 진행되고 있다. 부호어(codeword) 개수를 의미하며,   ⌊  ⌋ 능력을 나타낸 같이 신드롬 연산 Equation 오류 정정 블 여기 locator value



* 교신저자 : 강성진(sjkang@kut.ac.kr) 접수일 10년 3월 29일 수정일 10년 04월 26일

polynomial,  )을 찾기 위해 가장 많은 연산을 필요로 하며, 하드웨어 복잡도가 가장 높다. ω ( α i ) Codeword Received Syndrome S (x ) Key Equation σ (x ) Chien Search α i ⋅ σ ' ( α i ) Error Codeword Corrected And Computation Solver Correction ω (x ) Forney Algorithm FIFO [그림 1] RS 복호기의 블록도

RS 복호기에 관한 연구는 대부분 알고리즘에 관한 것이며, 많은 복호 알고리즘과 복호기 구조가 연구되어 왔다 [1, 2, 3, 4, 5, 6, 7, 8]. 이 중에서 수정된 유클리드(Modified Euclidean, ME) 알고리즘은 하드웨어의 규칙성이 우수하여 쉽게 구현이 가능 한 장점을 지니고 있다[4]. ME 알고리즘[2]은 차수 계산과 다항식 연산을 수행하는 processing element(PE) 블록을  개 사용하여 구현할 수 있

게재확정일 10년 06월 18일

으며, 이러한 구조는 하드웨어 규칙성 및 경로 지연(critical path)이 작아서 고속으로 동작하는 RS 복호기를 구현할 수 있다[4, 5]. [6]에서는 차수 계산이 필요치 않는 DCME(degree computationless ME)를 제안하였지만, 각 기 본 셀(basic cell)내의 feedback되는 부분과 모든 셀에 입력되 는 leading coefficient   ,   가 feedback되므로 상대적으로 고속 구현이 어렵게 된다. [7]에서는 DCME 알고리즘의 연시간과 basic cell을 개선하여 E-DCME 알고리즘을 하였다. [5]에서는 [4]의 구조를 개선하여 DCME 구조를 제안하였다. [8]에서는 [4]의 PE 구조를 개선하여 지막 PE 블록의 출력신호에서 차수 비교 MUX(multiplexer)가 필요없는 구조를 제안하였다. 본 논문에서는 [8]에서 제안된 PE 구조의 차수 계산 회로 를 FSM(finite-state machine)로 대치하여 하드웨어 복잡도 를 줄일 수 있는 구조를 제안한다. 본 논문의 구성은 2장에서 제안된 장에서는 제안된 PE 구조를 이용한 복호기 설계에 대하여 설명한다. 4장에서는 성능평가 결과를 제시하 고 5장에서 결론을 맺는다. 2. 제안된 PE 구조 [8]에서는 맨 마지막 PE 블록의 출력    와    의 차수를 비교하여 오류위치 다항식  과 오류값 다항식  을 결정하게 된다. 이러한 이유는 블록에 입력된      와      의 차수를 비교하여 다항식 스위칭 여 부를 결정한 후에 다항식 연산이 이루어지기 때문에 블록 외부에서 출력 다항식의 차수의 변화를 알 수 없기 때문이다. [4]에서는 각 PE 블록의 출력에서 항상     ≥     이 성립하도록, 블록의 출 력 다항식에 대하여 다항식 스위치가 이루어지는 구조를 제 안하였으며, 이를 통해 마지막 블록의 출력으로에서 바로  ,  를 얻을 수 있다. [4, 8]의 PE 구조에서 다항식 차수를 계산하는 블록은 스위 치(  )와  신호를 발생하기 위해서 필요하다. 블록 에서      ,      차수가 같고,      의 leading coefficient가 ‘0’이 아닌 경우에, 다항식 연산에서      의 최고차항 계수가 제거되어 차수가 므로,          가 되어 다항식 스위치 가 일어나게 된다.  신호는 블록의 출력 다항식    ,    의 차수가 오류정정 능력  보다 작을 때 발 생하여, 이후의 PE 블록이 동작하지 않도록 한다.

PE 블록에서  신호를 발생하기 위해서는      의 차수와      의 차수가 같은지를 판단할 수 있다면, 차 수 계산을 하지 않아도 됨을 알 수 있다. 따라서,          를 관찰함으로써 차수 계산을 하지 않고  신호를 발생시킬 수 있으며, 식 (1)과 같은 상 태 변수를 정의 할 수 있다. 지 제안                  (1) 알고리즘 마 여기에서,  ≤  ≤    이다. 즉,    와    의 및 차수 차이는    을 초과할 수 없다. [8]의 PE는      의 차수 또는      의 차수가 1씩 감소하는 구조이므로, 그림 2와 같은 상태도로 표현이 가능하다. 따라서, PE 블록은 그림 2와 같은 상태도를 갖는 FSM을 사용하여 차수 계산없 PE 구조를 설명하고, 3 이  신호를 발생할 수 있다. 그림 2에서,  는      의 leading coefficient가 ‘0’일 때 1이고, 그렇치 않으면 0인 RS(255,239,8) 신호이다. Legend : zq/sw 1/0 1/0 1/0 λ 0 0/1 λ 1 ⋅ ⋅ ⋅ λ t − 1 0/0 0/0 0/0 [그림 2]   의 상태도 PE [8]의 PE는     ≥     가 성립하므 PE 로,    의 차수가  보다 작으면  신호를 발생한다. 식 (1)에 정의된   로 부터    와    의 차수의 차 이를 알 수 있지만,    의 차수가  보다 작은지를 알 수 PE 가 없다. 따라서, 각 PE에서    의 변화를 관찰하고 있어 야 한다.    의 차수가 감소하는 경우는      의 PE leading coefficient가 ‘0’인 경우와 다항식 연산 후에          가 되어 다항식 스위치가 일 PE 어나는 경우이다. 따라서    의 차수가 감소하는 횟수를 카운트하는 상태변수를 식 (2)와 같이 정의할 수 있다. 만약,     라면    의 차수가 2번 감소함을 의미한다. 1감소하였으                          (2) PE 여기에서,  ≤   ≤    이다. 왜냐하면,  번째 PE블록 에서        이고         이면,

    가 되어야 하지만, 이 경우는    의 차수가    에서  만큼 줄어    의 차수가    이 되었음을 의미하 기 때문에,  신호가 발생하여    번째 이후의 PE 블록은 동작할 필요가 없으므로,   를 증가시킬 필요가 없기 때문이다. 따라서,       이면,        이다. 이로 부터 식 (3)과 같이   신호가 발생됨을 알 수 있다.   신호는       일 때 식 (3)과 같이 계산되며,       이면        이다.                              (3)     그림 3은 본 논문에서 제안하는 PE 블록의 구조이다. 그 림 3에서 FSM은 그림 2의 상태도를 가지며, ‘Y’ 표시의 박 스는 식 (2)와 식 (3)을 통해   와   신호를 발생하는 회 로이다. 그림 3의 ‘X’ 표시의 박스는 제어 신호  ,   ,   를 생성하는 조합회로이며, leadR, leadQ는 각각      ,      의 leading coefficient를 나타낸다. 제 어신호 zq는    일 때 ‘1’이 된다. 그리고,   와   는 각각 식 (4), (5)와 같이 계산된다.          (4)           (5) ∆ i-1 ∆ i zq FSM sw μ i-1 μ i sw Y zq zq D stop i stop i-1 leadQ X cntrA cntrB R i-1 D D 0 1 0 cntrA R i 1 leadQ sw Q i-1 D leadR D 0 1 1 cntrB Q i 0 L i-1 D D 0 1 0 cntrA L i 1 leadQ sw leadR 1 cntrB U i-1 D D 0 1 U i 0 start i-1 start i D D [그림 3] 제안된 PE 블록 구조

3. RS(255,239,8) 복호기 설계 RS(255,239,8) 부호의 발생 다항식  는 식 (6)과 같다.          (6)                                                    RS 부호기는 239byte의 정보 심볼을 입력받아서, 발생다 항식  를 이용하여 RS 패리티 16byte를 구한 후에, 정보 심볼 239byte와 패리티 16byte를 합하여 총 255byte의 부호 어를 발생시킨다. RS(n,k,t)부호의 송신된 부호어(codeword) 다항식을  , 수신된 부호어 다항식을  , 에러 다항식을   라 하면,  는 식 (7)과 같다.       (7)          ⋯       RS 복호기는 수신된 부호어로부터 식 (8)와 같이 신드롬 (Syndrome)   를 계산한다.                    (8)  KES 블록은 신드롬   로부터 식 (9)의 키방정식 연산 을 통해 오류위치 다항식  와 오류값 다항식  을 계산한다[1, 2, 3, 4].  ⋅      (9) 여기에서,  의 차수는  이고,  의 차수는    이다. RS(255,239,8) 복호기를 위한 KES 블록은 2장에서 제 안된 PE 블록을    개 연결하여 구현할 수 있다. ∆ 0 μ 0 stop 0 ω(x)

L 0 (x) xU 0 (x) start 0 [그림 4] 제안된 PE 블록을 이용한 KES 블록도

여기에서,   는 ME 알고리즘에서       ,       이므로,     이다. 그리고,     ,     이며,   는 [2]에서와 같이 발생된다. 즉,    의 최고차항을 나타내는 시간동안에만 1이고, 나머지 시간에는 0이다.      ,      이다. KES블록의 출력인 오류위치 다항식  와 오류값 다항식  는 각 각 식 (10), 식 (11)과 같다.      (10)      (11) KES 블록에서  와  가 계산되면, Chien 탐색과 Forney 알고리즘을 이용하여 식 (12)과 같이 오류 정정이 가 능하다[3].                ′              (12)        여기에서,   ⋯ 이고,   는 오류가 정정된  번째 부호어 심볼이다. Chien 탐색과 Forney 알고리즘은 [4]에서 와 같이 간단하게 구현될 수 있다. 4. 성능평가

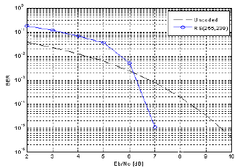
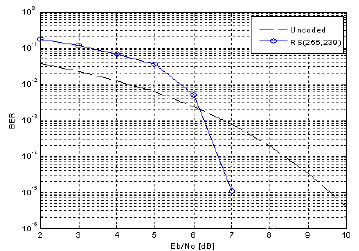
제안된 ME알고리즘 구조의 다양한 오류패턴에 대한 유 효성을 검증하기 위해 RS(255,239,8) 부호의 복호기를 C프 로그램을 작성하여 시뮬레이션을 수행하였다. 그림 5는 AWGN(Additive White Gaussian Noise)채널에서 BPSK(Binary Phase Shift Keying)변조를 사용했을 때, RS(255,239)부호의 BER성능 곡선이다. RS(255,239)부호는 비트오류확률   에서 약 2.5dB의 부호이득을 가진다.

[그림 5] RS(255,239) 부호의 BER 성능

본 논문에서는 제안된 PE 구조를 이용하는 RS(255,239,8) 복호기를 Verilog HDL를 사용하여 구현하였으며, 삼성 65nm library로 합성하였다. 표 1은 본 논문에서 제안된 구조 의 구현 결과를 비교한 것이며, 그림 1의 RS 복호기 중에서 KES 블록만을 비교하였고, 다른 블록은 [4, 5]와 동일하다. [7]에서 제안된 DCME 구조는 latency와 gate count 측면에 서 가장 우수하지만, 고속 복호에는 적합지 않음을 알 수 있 다. 제안된 PE 구조와 유사한 구조를 갖는 [4, 5]의 구현 결과 와 비교하면, 유사한 동작 주파수를 가지면서 본 논문에서 제 안된 구조가 [4]에 비해 약 13%정도 gate count가 줄어드는 것을 알 수 있고, latency도 [4, 5]에 비해 현저하게 줄어드는 것을 알 수 있다. [표 1] RS(255,239,8) 복호기 구현 결과 Architecture proposed pDCME[5] ME[4] DCME[7] Technology 65nm 0.13um 0.13um 0.18um KES 4,0060 46,200 55,500 18,000 (gate count) Clock 660 660 625 200 rate(MHz) Latency 32 80 80 16 (clock) 5. 결론 본 논문에서는 차수 계산을 하지 않고 FSM을 이용하여 ME 알고리즘을 구현할 수 있는 PE 구조를 제안하였다. 제안 된 구조는 차수 계산 회로 대신 FSM을 이용하기 때문에, 고 속 복호기 구현이 가능할 뿐 만 아니라 하드웨어 복잡도를 줄 일 수 있다. 제안된 구조를 이용하는 KES 블록은 660MHz의 고속 clock에서 동작하며, [5]에 비해 약 13%정도 gate count가 줄어듬을 확인하였다. 참고문헌