http://dx.doi.org/10.5762/KAIS.2016.17.7.529 ISSN 1975-4701 / eISSN 2288-4688

Journal of the Korea Academia-Industrial cooperation Society Vol. 17, No. 7 pp. 529-535, 2016

이승현 1 , 한진태 2* 1 선문대학교 토목공학과, 2 한국건설기술연구원

A Study on Comparison of Strength Parameters of Hydrostatic Pressure-Dependent Yield Criteria

Seung-Hyun Lee 1 , Jin-Tae Han 2* 1 Department of Civil Engineering, Sunmoon University 2 Korea Institute of Construction Technology

요 약

Mohr-Coulomb Drucker-Prager 는 원이 Mohr-Coulomb 내부마찰각에 비례하였는데 내부마찰각이

Mohr-Coulomb 강도정수가 Drucker-Prager 최소값이

이론적 연구를 통하여 정수압의 영향을 받는 항복기준인 Mohr-Coulomb 항복기준과 Drucker-Prager 항복기준의 강도 정수를  - 평면에 대해 일치시킴으로써 강도정수간의 상관관계를 분석해 보았다 . Drucker-Prager 강도정수  와  를 강도정수인  와  를 이용하여 표현하였는데  는  ,  의 함수로 표현되었고  는  만의 함수로 표현되었다 . 강도정수  값은 흙의 내부마찰각이 커짐에 따라 증가함을 알 수 있었는데 Drucker-Prager 항복기준을 나타내 항복기준에 외접 및 내접하는 경우의  값을 나타내는   와   값에 대하여 평균값인   의 값은 10  인 경우 약 0.07 이었으며 내부마찰각이 45  인 경우 약 0.29 이었다 . 또한 ,     값은 내부마찰각에 비례하였는데 내부마찰각이 10  인 경우 약 1.12 이었으며 내부마찰각이 45  인 경우 약 1.62 이었다 . 강도정수  에 미치는 영향을 살펴보았는데 본 연구에서 가정한 흙의 점착력 중 10kPa 인 경우를 제외하고 흙의 내부마찰각의 영향을 거의 받지 않고 전체적으로 흙의 점착력에 영향을 받음을 알 수 있었다 . 일정한 점착력에 대하여 내부마찰각이 증가함에 따라 일축압축시 및 일축인장시의 Mohr-Coulomb 항복기준에   값은 감소하였다 . 또한 내부마찰각이 증가할수록 Mohr-Coulomb   로부터   와   사이의 편차가 내부마찰각이 증가함에 따라 커짐을

의한 축차응력인   와   그리고 두 값의 평균값인 항복궤적을 나타내는 육각형이 더욱 불규칙해져 알 수 있었다 .

Abstract

In this theoretical study, the strength parameters of the Drucker-Prager yield criterion and Mohr-Coulomb yield criterion were set to equal values, in order to analyze the correlation among the parameters.

The Drucker-Prager strength parameters  and  were  . Specifically it can be seen that is function of  , 

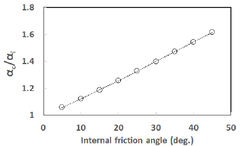
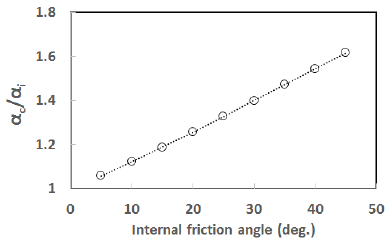
   parameter  increases as the internal friction angle of soil increases.   which is the average of   and   was proportional to internal friction angle in which   and   are  values corresponding to the circles of the Drucker-Prager yield cirteria circumscribes and inscribes the Mohr-Coulomb yield criterion respectively. The values of the   was 0.07 and 0.29 which correspond to the internal friction angle of 10  and 45  respectively. In addition, value of     was proportional to internal friction angle of soil and the values of     1.12 and 1.62 which corresponds to internal friction angle of 10  and 45  respectively.The influence of the Mohr-Coulomb strength parameters on the Drucker-Prager strength parameter  was investigated and it was found that  was mainly influenced by the cohesion of the soil, except in the case of the minimum assumed value of  of 10kPa. The deviator stresses,   and   , which correspond to the cases of the Mohr-Coulomb yield criterion under uniaxial compression and uniaxial tension, respectively, and   , which is the average value of   and   , decrease as the internal friction angle increases. Furthermore, the hexagon, which represents the Mohr-Coulomb yield locus, becomes more irregular, and the deviations of   and   from   also increase, as the internal friction angle increases. Keywords : Drucker-Prager yield criterion, Mohr-Coulomb yield criterion,  -plane, Parameter  , Parameter 

* Corresponding Author : Jin-Tae Han(Korea Institute of Construction Technology) Tel: +82-31-910-0259 email: jimmyhane@kict.re.kr Received May 3, 2016 Revised July 6, 2016 Accepted July 7, 2016 Published July 31, 2016

529

한국산학기술학회논문지 제17권 제7호, 2016

1. 서론 식 (4)를 통해 축차응력벡터의 크기는 일정함을 알 수 있으며 Fig. 1에 나타나 있는 바와 같이 von Mises 항복 등방 금속재료의 항복조건으로 일반적으로 가장 많이 궤적은 반지름이      인 원이 된다. 쓰이는 항복기준은 Tresca 항복기준[1]과 von Mises 항 복기준[2]으로서 Taylor and Quinney [3]는 일련의 시험   ′ 을 통해 Tresca 항복조건과 von Mises 항복기준이 금속 의 실제거동을 잘 모사함을 입증한 바 있다. Tresca 항복  기준은 재료에 발생하는 최대 전단응력이 특정한 임계값 에 도달할 때 항복이 일어난다는 것으로 식 (1)과 같이 표현된다.

                                    

(1)

Tresca 항복기준을 응력불변량으로 표현하는 경우는 표현식이 매우 까다롭게 나타나므로 잘 쓰이지는 않는 다. von Mises 항복기준은 식 (2)과 같이 표현된다.

in the  -plane

                          (2) 접하는 따라서 원이 von 됨을 Mises 알 항복궤적은 수 있다. Tresca Tresca 항복기준과 항복궤적에 von 외 Mises 항복기준은 정수압과 무관하므로 Tresca 항복면 식 (2)를 응력불변량을 이용하여 나타내면 식 (3)과 은 중심이 공간대각선상에 있는 공간대각선방향으로의 같이 표현된다. 정육각형기둥이 되고 von Mises 항복면은 중심이 공간 대각선상에 있는 공간대각선 방향으로의 원기둥이 된다.       (3) Mohr-Coulomb 항복기준과 Drucker-Prager 항복기준은

식 (3)에서   는 축차응력 불변량(deviatoric stress 하는 항복기준인 Mohr-Coulomb 항복기준과 Drucker-Prager invariants)을 의미한다[4]. 식 (1)로 표현되는 Tresca 항 항복기준을 일치시키고자 할 때 Drucker-Prager 강도정 복기준과 식 (3)으로 표현되는 von Mises 항복기준은 정 수가 Mohr-Coulomb 강도정수에 어떻게 영향을 받는지 수압과 무관한 항복기준으로 이들은 각각 정수압에 의존 를 매개변수연구를 통해 살펴보고자 하였다. 적인 항복기준인 Mohr-Coulomb 항복기준과 Drucker-Prager 항복기준과 밀접한 관련이 있다. Tresca 항복기준을 -평면에 나타내면 Fig. 1의 정육각형과 같 2. 정수압에 의존하는 항복기준 게 된다. 이때   방향으로의 일축압축 항복응력   를  -평면에 투영시킨 길이는      가 된다. 식 (2)의 좌 Tresca 항복기준과 von Mises 항복기준은 정수압의 변을 축차응력(    )을 이용하여 나타내고 우변의 를 영향을 받지 않는 것으로 금속의 소성모델에 적합하다.         인 관계를 적용하여 나타내면 식 (4)와 같이 암석과 흙 그리고 콘크리트와 같은 재료의 경우 항복은 표현된다. 정수압응력과 밀접한 관련이 있다. Drucker-Prager 항복 기준[5]은 von Mises 항복기준을 간단히 수정한 것으로                      (4) Mises 식 (5)와 항복기준에 같이 정수압을 도입하고 의미하는 있다. 응력불변량   을 von 530

정수압에 의존하는 항복기준의 강도정수 비교연구

고 있다.

                   

(5)

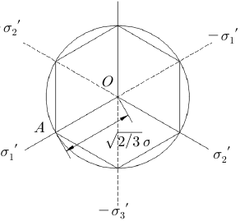
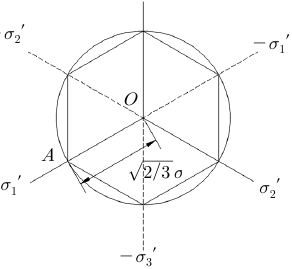
식 (5)에서 는 Drucker-Prager 강도정수이다. 식 (5)         (7) 를 Haigh-Westergaard 좌표[6,7]를 이용하여 나타내기 위해        ,         관계를 식 (5)에 적용하면 식 (7)에서 , 는 각각 점착력과 흙의 전단저항각을 식 (6)과 같이 표현된다. 의미한다. 그리고   와   은 각각 파괴면에 작용하는 전 단응력과 수직응력을 의미한다. Mohr-Coulomb 항복기            (6) 준이 의미하는 바는 압력   이 커질수록 재료가 견딜 수 있는 전단응력도 커진다는 것이다. Mohr-Coulomb 항복 식 (6)은   인 경우 von Mises 항복기준이 되며 기준은 Tresca 항복기준의 일반화된 버전이라 할 수 있 Fig. 2 (a)에 나타나 있는 바와 같이 반지름    의 원 는데   이고   인 경우 Tresca 항복기준이 되기 이 되며 식 (6)에서 정수압응력 를 수평축으로 하고 축 때문이다. 파괴시의 응력상태가   >  >  인 경우의 차응력 를 연직축으로 하는 Haigh-Westergaard 좌표를 Mohr 응력원을 (  ,   ) 공간에 나타내면 Fig. 3과 같다. 이용하여 나타내면 Fig. 2 (b)와 같다.    ′ 



  

   

 

 

   



  ′



  ′ meridian plane

(a)  -plane



   

Fig. 3의 기하학적 형태를 고려하여 Mohr-Coulomb 항복기준을 식 (8)과 같이 주응력을 이용하여 나타낼 수 있다.

   

               

(8)



     

3. 정수압에 의존하는 항복기준의 특성비교

(b) Meridian plane

Haigh-Westergaard 좌표계에 의한 Mohr-Coulomb 항복기준은 식 (9)와 같이 표현된다.

Fig. 2를 통해 알 수 있는 바와 같이 Drucker-Prager 항복기준의 3차원적 모양은 원뿔이 된다. Mohr-Coulomb 항복기준은 식 (7)에 나타낸 Coulomb[8]의 식에 근거하

                     (9)                   

531

한국산학기술학회논문지 제17권 제7호, 2016

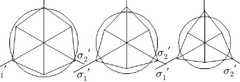
식 (9)로부터   ,   를 대입하면 식 (10)과 같 따라서 Mohr-Coulomb의 항복면을 3차원적으로 고려 이 일축압축항복시의 축차응력,   를 구할 수 있다. 하면 불규칙한 육각뿔이 됨을 알 수 있다. Drucker-Prager 항복면과 Mohr-Coulomb 항복면을 일치시키기 위하여        먼저 Fig. 4의 장축의 꼭지점과 Fig. 2(a)에 나타낸 원의         (10) 반지름을 일치시킨 경우를 고려하면 Drucker-Prager 재 료정수 와 를 각각 식 (12) 및 식 (13)과 같이 구할 또한,   ,   를 식 (9)에 대입하면 식 (11)과 수 있다. 같이 일축인장항복시의 축차응력,   를 구할 수 있다.                         (12)         (11)                (13) -평면에   와   를 나타내고 대칭성을 고려하면 Fig. 4와 같이 불규칙한 육각형으로 표현되는 Mohr-Coulomb 다음으로 Fig. 4의 단축의 꼭지점과 Fig. 2(a)에 나타 항복기준을 얻을 수 있다. 낸 원의 반지름을 일치시킨 경우를 고려하면 Drucker-Prager 재료정수 와 를 각각 식 (14) 및 식 (15)와 같이 구할 수 있다.

                               

(14) (15)

  ′

식 (12)~(15)를 통해 알 수 있듯이 Drucker-Prager 재료정수 는 Mohr-Coulomb 재료정수  및 와 관련 이 있음을 알 수 있으며 는 Mohr-Coulomb 재료정수



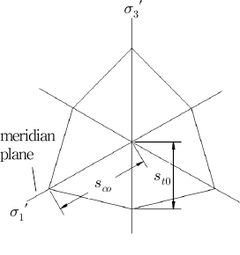
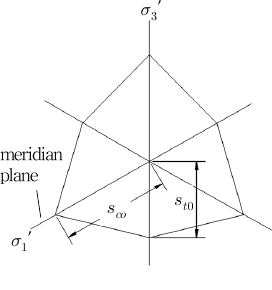
와   그리고 그들의 평균값인   의 변화양상을 살펴 보기 위해 내부마찰각을 5에서부터 45까지 5씩 Mohr-Coulomb 항복기준을 식 (9)를 참고하여 자오 증가된 값으로 가정하였는데 계산결과는 Fig. 6과 같다. 평면(meridian plane)에 나타내면 Fig. 5와 같다. 또한     의 변화양상을 흙의 내부마찰각에 대하여 나 타내면 Fig. 7과 같다. 

 -plane

   



    

532

정수압에 의존하는 항복기준의 강도정수 비교연구

(b)  

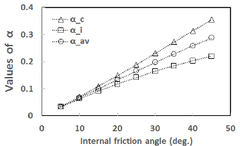
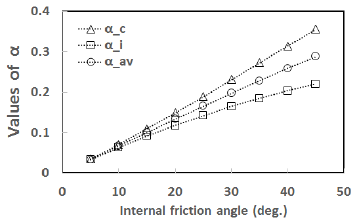
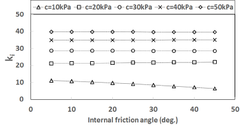
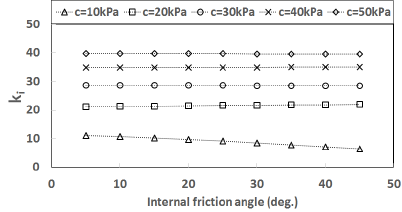
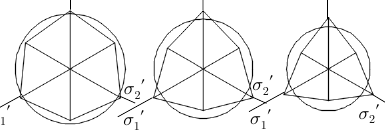
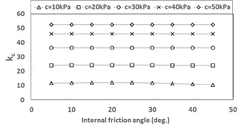
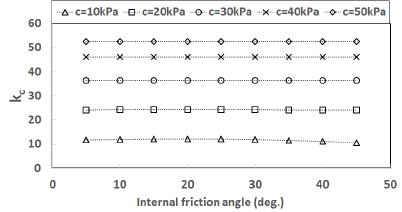
Fig. 6을 통해 알 수 있듯이   의 값이   보다 큼을 Fig. 8을 통해 알 수 있듯이 Drucker-Prager 강도정수 알 수 있으며 값들은 모래의 내부마찰각이 커짐에 따 는 가정한 흙의 점착력 중 최소값인 10kPa인 경우를 라 증가함을 알 수 있는데   의 경우 내부마찰각이 10 제외하고 흙의 내부마찰각의 영향을 거의 받지 않고 흙 의 점착력에 영향을 받음을 알 수 있다. -평면에 인 경우 약 0.07이며 내부마찰각이 45인 경우 약 0.36 이다.   의 경우 내부마찰각이 10인 경우 약 0.06이며 Mohr-Coulomb 항복기준을 나타내보고자   와   그 내부마찰각이 45인 경우 약 0.22이다.   의 경우 내 리고 이들 값의 평균값은   를 계산해 보았는데 Table 1에 나타내었다. Table 1의 계산결과로부터 점착 부마찰각이 10인 경우 약 0.07이며 내부마찰각이 45 력()이 30kPa인 경우에 대하여 내부마찰각()이 10, 인 경우 약 0.29이다. Fig. 7을 통해 알 수 있듯이 내부 마찰각에 따른     의 값은 내부마찰각에 비례함을 알 30 그리고 45인 경우의   와   그리고   를 반지름으로 하는 원을 -평면에 나타내면 Fig. 9와 같다.

  ′

  ′

  ′



였다. 가정한 점착력에 대하여 흙의 내부마찰각에 대한   와   를 나타내면 각각 Fig. 8(a) 및 Fig. 8(b)와 같다.

(a)   

(b)    (c)   

(a)  

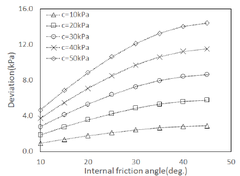
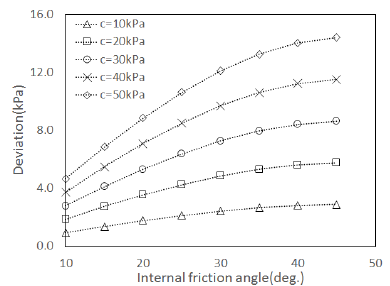
Table 1과 Fig. 9를 통해 알 수 있듯이   와   그리 고   값은 내부마찰각이 증가할수록 감소함을 알 수 있다. 또한 Fig. 9를 통해 알 수 있듯이 내부마찰각이 증 가할수록 Mohr-Coulomb 항복궤적을 나타내는 육각형 이 더욱 불규칙해짐을 알 수 있어   로부터   와   사이의 편차가 내부마찰각이 증가함에 따라 커짐을 알 수 있다. Table 1로부터 계산에 고려한 모든 점착력 에 대하여 내부마찰각에 따른 편차(deviation)를 나타내

533

한국산학기술학회논문지 제17권 제7호, 2016

 (deg)                  (kPa)                            (kPa)                            (kPa)          

10 17.1 34.1 51.2 68.3 85.3 15.2 30.4 45.6 60.8 76.0 16.1 32.3 48.4 64.5 80.7

15 17.3 34.5 51.8 69.1 86.3 14.5 29.0 43.6 58.1 72.6 15.9 31.8 47.7 63.6 79.5

20 17.3 34.6 52.0 69.3 86.6 13.8 27.5 41.3 55.1 68.9 15.5 31.1 46.6 62.2 77.7

25 17.2 34.5 51.7 68.9 86.1 13.0 25.9 38.9 51.9 64.9 15.1 30.2 45.3 60.4 75.5

30 17.0 33.9 50.9 67.9 84.9 12.1 24.2 36.4 48.5 60.6 14.5 29.1 43.6 58.2 72.7

35 16.5 33.1 49.6 66.2 82.7 11.2 22.5 33.7 44.9 56.1 13.9 27.8 41.7 55.5 69.4

40 15.9 31.8 47.8 63.7 79.6 10.3 20.6 30.9 41.2 51.5 13.1 26.2 39.3 52.4 65.6

45 15.1 30.2 45.3 60.4 75.5 9.3 18.7 28.0 37.4 46.7 12.2 24.5 36.7 48.9 61.1

4. 결 론

면 Fig. 10과 같다. 여기서 편차는   와   사이의 차를 의미한다.

이론적 연구를 통하여 정수압에 영향을 받는 항복기 준인 Mohr-Coulomb 항복기준과 Drucker-Prager 항복 기준의 강도정수를 -평면에 대해 일치시킴으로써 강도 정수간의 상관관계를 분석해 보았다. 연구를 통해 얻은 결론은 다음과 같다. (1) 본 연구를 통해 Drucker-Prager 강도정수 와  를 Mohr-Coulomb 강도정수인 와 를 이용하여

는 만의 함수로 표현되었다. (2) 흙의 내부마찰각에 대한 Drucker-Prager 강도정 수 의 변화양상을 살펴보았는데 값은 모래의 내부마찰각이 커짐에 따라 증가하였다. Drucker- Prager 항복기준을 나타내는 원이 Mohr-Coulomb 항복기준에 외접 및 내접하는 경우의 값을 나타 내는   와   값들의 평균값인   의 경우 내부 마찰각이 10인 경우 약 0.07이었으며 내부마찰 각이 45인 경우 약 0.29이었다. 또한     의 값은 내부마찰각에 비례하였는데 내부마찰각이 10인 경우 약 1.12이었으며 내부마찰각이 45 인 경우 약 1.62이었다. (3) Mohr-Coulomb의 강도정수가 Drucker-Prager 강 도정수 에 미치는 영향을 살펴보았는데 본 연구 에서 가정한 흙의 점착력 중 최소값인 10kPa인

Fig. 10을 통해 알 수 있듯이 동일한 내부마찰각에 대 하여 점착력이 커짐에 따라 편차도 커짐을 알 수 있으며 특정 점착력에 대하여 편차는 내부마찰각이 커짐에 따라 증가함을 알 수 있다.   kPa이고   인 경우 의 편차값은 0.9kPa 이며 점착력 및 내부마찰각이 커짐 에 따라 편차는 커져서   kPa이고   인 경우 의 편차값은 14.4kPa 이다. 이러한 결과는 Mohr-Coulomb 항복기준을 Drucker-Prager 항복기준으 로 근사시킬 경우 두 가지의 항복기준을 신뢰성 있게 일 치시켜 볼 수 있는 편차의 한계를 규정하는데 도움이 될 것으로 생각된다.

534

정수압에 의존하는 항복기준의 강도정수 비교연구

이 승 현 (Seung-Hyun Lee)

[정회원]

• 1988년 8월 : 서울대학교 토목공학 과 (공학사) • 1991년 2월 : 서울대학교 토목공학 과 (공학석사) • 1997년 2월 : 서울대학교 토목공학 과 (공학박사) • 2000년 3월 ~ 현재 : 선문대학교 건축사회환경학부 교수

<관심분야> 토질역학, 기초공학

한 진 태 (Jin-Tae Han)

[정회원]

경우를 제외하고 흙의 내부마찰각의 영향을 거의 받지 않고 전체적으로 흙의 점착력에 영향을 받 음을 알 수 있었다. (4) 일정한 점착력에 대하여 내부마찰각이 증가함에 따라 일축압축시 및 일축인장시의 Mohr-Coulomb 항복기준에 의한 축차응력인   와   그리고 두 값의 평균값인   값은 감소하였다. 또한 내부 마찰각이 증가할수록 Mohr-Coulomb 항복궤적을 나타내는 육각형이 더욱 불규칙해져   로부 터   와   사이의 편차가 내부마찰각이 증가함 에 따라 커짐을 알 수 있었다. (5) 본 연구를 통하여 Mohr-Coulomb 항복기준을 Drucker-Prager 항복기준으로 근사시킬 경우 두 가지의 항복기준을 신뢰성 있게 일치시켜 볼 수 있는 편차의 한계를 규정하는데 도움이 될 것으 로 생각된다.