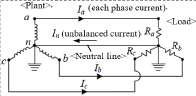
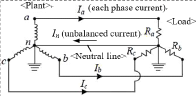
가공 배전선의 전자유도전압에 대하여 대지 귀로전류 원리를 반영한 중성선 차폐계수 계산 방법

14%
   ,
. 1/10가공배전선에 의하여 통신선에 유도되는 전압을 계산하는데에 있어서 기존의 중성선 차폐계수를 단일의 값으로 사용 인한 과다 오차 발생 문제를 해결하기 위하여 실제 배전 구간의 전주 접지 마다 발생하는 누설전류에 의한 대지귀로 영향이 반영된 일반식이 개발된 바 있다 각 전주 접지에서 발생하는 누설전류의 근원은 중성선에 유입되는 불평형전 . 그러므로 누설전류와 그 합인 대지귀로전류는 이 불평형전류에 대한 각 전주 위치에서의 누설율들의 합성적 인수 표현이 가능하다 본 논문에서는 결국 원래의 일반식을 누설율의 관점에서 전개하여 좀더 실용적인 의미를 갖도록 . 이렇게 하면 유도의 원천 전류인 중성선 불평형전류에 대한 누설전류 요율만의 합성 인수로 대체된 중성선 차폐계수 계산식이 도출된다 이 계산식의 의미는 전 배전 구간에서 중성선에 의한 차폐 효과가 일정한 것이 아니라 유도 구간의 위치 따라서 원래 유도를 발생시키는 전류인 중성선 불평형전류의 양이 달라지는 요율을 말한다는 것이다 이와 같은 방식으로 계산하였을 때 기존 방식에 비하여 과소 예측에 대하여는 증진율을 과다 예측에 대하여는 평균 수준으로의 감소 기대할 수 있다
   .
연구는 2016년도 미래창조과학부 및 정보통신기술연구진흥센터의 정보통신·방송연구개발사업의 일환으로 수행하였음 [R0166-16-1020, 방송통신 설비 기술기준 연구]. Corresponding Author : Sangmu Lee(ETRI) +82-42-860-4925 email: Received February 23, 2016 Revised (1st July 1, 2016, 2nd July 5, 2016, 3rd July 6, 2016) Accepted July 7, 2016 Published July 31, 201686 [1].
    (1)과
(1)
   L : 배전선 : 60Hz에 M: 60Hz에
l : : 배전선 21 : 3 : 전기통신선의 7 : 통신케이블 )는 1로
   [2]의

   [2]에서
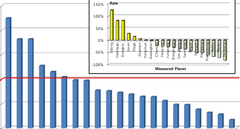
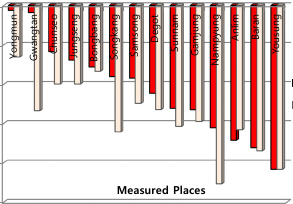
21 (1) 1과배전선에 의하여 주변의 통신선에 유도되는 전 식으로 가공배전선에 의한 유도전압을 계산하고 있다 계산할 때에 가공 배전선의 구성 선로인 중성선에 문제의 중성선 차폐계수를 적용하여야 할 유도전압 차폐효과가 적용될 수 있다. 이에 대하여 유도전압 계산식은 같다. 계산하는 방법을 제공하는 국가 기술기준(국립전파연 고시)에서 중성선 차폐계수를 선종 분류에 따라 몇                 수치로 제시하고 있다[1]. 그러나 우리나라의 경우 V 정상운전시 유도종전압(V) 중성선은 매 전주 마다 접지속 대지로 누설되기 때문에 ω 대한 각속도[rad/sec] 진행됨에 따라 차폐 효과도 변화하게 된다. 따라 대한 전력선과 전기통신선의 상호인덕턴 중성선 차폐계수를 단적 수치로 사용하는 것은 통신 스(H/km) 받는 유도 구간이 전체 배전 구간 중 어디에 위치 전력선과 전기통신선의 병행거리(km) 하느냐에 따른 변화가 반영되지 못하기 때문에 평균적인 I n 중성선에 흐르는 불평형 전류(A) 의미로서는 사용할 수 있을지라도 유도를 받는 통 K 배전선 중성선의 차폐계수 위치에 따라서는 실제 유도전압에 대한 계산값의 K 차폐계수 커질 수 밖에 없는 문제가 있다. 이와 같이 중성 K 조수에 의한 유도 저감계수 접지를 통하여 누설되는 각 위치에서의 대지귀로전류 영향이 반영된 유도전압 계산 적용 방법에 대하여 참 배전선 중성선에 대한 차폐계수(K 21 표 주어져 논문에서 다룬 바 있다. 있다. 이것은 전력선종에 의한 중성선의 단면적에 따른 논문에서는 참고문헌 제시한 누설전류가 차폐계수를 산정해 놓은 것이다. 유도를 발생시키는 전류를 계산하는 일반적인 방 좀더 간편하게 쓸 수 있는 실용식으로 개발한 내용 Power Line Class( mm2 ) Shielding Coefficient 제시한다. 여기서 말하는 실용식이란 통신선 유도 구 ACSR 160 0.63 각 지점 위치에서 유도를 발생시키는 전류를 전주 〃 95 0.65 〃 58 0.68 감안하지 않고 단적 수치로 나타낸 중성선 차폐 〃 32 0.75 근원인 중성선 불평형전류가 공통 인수로서 결합 누설전류 요율만의 합성 관계로 나타낼 수 있고 이 2.2 현행 식의 계산 정확도 요율들의 합성 관계를 중성선 차폐계수 계산식의 관점으 실제 배전선 유도 병행 구간 개소에 대하여 식 인수 분할한 것이다. 로 계산된 유도전압과 실제로 측정한 유도전압과의 대비 이러한 과정의 도출을 위하여 기존의 측정 개소 데이 분석을 하여보면 그림 같다. 활용하여 현재 사용되고 있는 계산식 오차 문제의 정량성을 재조명하고 어떻게 누설전류 합의 일반적 표현 Estimation Rate 1200% 순수 누설전류 요율들만으로 인수화된 중성선 차폐계 Over/Under Rate 1100% 1000% 계산식이 도출되는지, 그 산식 개발 과정을 설명한다. 800% 900% 700% 600% 500% 만들어진 실용적 관계식을 적용하여 계산하였을 400% 300% 200% 100% 기존 측정 데이터를 활용하여 분석한 결과 충분 -100% -200% 0% Haenggu Bongkoc Hwajang Edong Jusan Dega Gwansul Yongmun Bongbang Jungseng Chunseo Samsong Degot Gwangtan Gamjung Sunnam Anlim Songkang Baran Yousung Nampyung 개선 효과가 있음을 보여준다. Measured Places
   1100% 1000% 900% 800% 700% 600% 500% 400% 300% 200% 100% 0%
[Measured Places]현행 계산식 시스템87
   100%이면

   1에서 1100%에

   100%에
2와
   I L4 I L3 I L2 I g4 I g3 I g2

   2에서
3 )가
    (1)에서

   )로부터
계산값이 실측값과 같다는 것을 말하 져나간 I n2 가 중성선으로 분기되며 I L2 는 이전 누설되어 정확하게 예측했음을 의미한다. 그런데 그림 대지 귀로 전류로 흐르는 I g1 과 합쳐져서 I g2 로서 흐른다. 살펴보면, 예측율 최대가 달하여 실측값에 대 이와 같은 메커니즘으로 대지 귀로 전류가 누적적으로 10 배를 예측하고 있으며 낮은 예측의 경우 약 합성되어 변전측으로 흐르게 된다. 전주에서의 누 밖에 예측되지 못하고 있다. 그림 내 우상의 별도 설전류를 일반식으로 표현하면 식 쓸 수 있다[2]. 도표는 예측율 대하여 과다 예측 또는  예측율을 나타낸 것이다. 즉 각 측정 개소의 「예측               100%」로 계산된 것이다.                              전주수) 누설전류 계산의 일반식 가공배전선로의 회로적 구성 형태는 그림 같다[2]. 식     는 전주에서 변전측으로 바라 보는 테브닌 등가임피던스이고   는 전주에서의 누설율을 의미한다. Phase current ( I x :I a , I b , I c ) Z L 3.2 누설율만의 합성 전개 I n 3.2.1 단위 회로의 누설율 전개 모델 I n5 5 Z 4 I n4 4 Z 3 I n3 3 Z 2 I n2 2 Z 1 I n1 1 가공 배전 선로에서 최초 유입된 중성선 불평형전류 I L5 I L1 g5 R 5 R 4 R 3 R 2 I g1 R 1 가 선로를 진행하면서 누설되는 요율에 의해 각 전주 위 치에서 합성되는 요율 관계는 그림 선로 위치 모델을 이용하여 전개하여보면 같이 된다. 편의상 대지로 누설되기 전 흐르는 불평 전류가 흐르는 하나의 선로처럼 등가적으로 나타냈으 실제는 전력선 상의 부하 불평형에 의하여 중성선 흐르는 전류(I n 형성되는 것은 작은 상자 안의 그 림에서와 같다. 이 불평형전류가 식 유도를 발생 기본 전류로 사용되는 것이고 변전소로 귀로되는 중성선의 다중 접지에 의하여 누설되는 양 만큼 중 차폐효과가 위치에 관계하여 줄어들게 되는 것이 논문에서는 주어진 I n 에 대하여 누설 요율에 의한 분석하는데 의미를 둔 것이다. 부하(Z L 잔류되어 나온 불평형전류인 최초 I n 첫번째 전주 접속점 1에서 중성선과 접지측으로 분 접지측으로 분기된 전류가 누설 전류이다. 접지 분기된 전류 I L1 은 접지저항 R 1 을 통하여 대지로 이 샘플 모델에서 결과적으로 각 전주에서의 누설전 유입되고 대지 귀로전류 I g1 이 되어 변전측으로 흐른다. 류에 의한 대지귀로전류는 원래 유입되었던 중성선 불평 형전류(I n 대하여 당해 위치까지 전주들에서 발생한88
   k번째 (2)로
(2)
   (k: 1~N-1, N: (2)에서 k번째 k번째 3의 분할 예로서 식 (3)과 I n I n ′ = I n − α 1 I n I n ′′ = I n ′ − α 2 I n ′ I n ′′′ = I n ′′ − α 3 I n ′′ α 1 I L 1 α 2 I L 2 α 3 I L 3 α 4 I g1 I g2 I g3
                                                               ( 3) )에3.2.2 누설율 전개의 확장과 합성 인수
   2
전주에서의 누설전류 I Lk 와 그 직전 전주까지 누설전류 들의 합 ΣI Lk- 로 나누어 정리하면 각각 표 및 표 3과 같이 된다. 결국 표 2 및 표 3의 요율 전개를 인수식으 로 표현하면 ( 4) 및 (5)와 같이 된다. (4)
   (단,   )
(5)                                                
   3.3 중성선 차폐계수 계산식의 분리 3.3.1 대지귀로전류 합성 k번째 전주에서의 대지귀로전류 I gk 는 k번째 전주에 서의 누설전류 I Lk 와 그 직전 전주까지 누설전류들의 합 의 합이므로 식 (6)과 같이 정리된다[3].
I Lk                                                                                                                                                                                                                                                                                                                                                                                                                                                                  (단,    ) (6)    
   , k번째
또한, I Lk 와 ΣI Lk- 이 두 개의 합은 결국 전주에 서의 총 대지귀로전류(k번째 전주까지 모든 누설전류들 의 합)가 된다.4에
   3
(7)에서 pq )로 89 (9)Σ I Lk-                                                                                                                                                                                                                                                                                                                                         3.3.2 평균 기유도전류 그림 예시된 유도 구간 병행 거리 을 등분된 각 구간  ′ 으로 나누어 본다면 통신선이 받는 유도전압 은 분절된 각 구간 마다의 대지귀로전류-대지귀로전류가 곧 유도를 발생시키는 전류, 즉 기유도전류이다-에 의한 유도전압의 합이 되는데 이것은 식 전개된 바와 같이 전체 병행 거리에 대하면 유도 구간 내 각 전주 에서 나가는 대지귀로전류의 총합(q점에서 나가는 대지 귀로전류는 제외된다)을 전주에 의한 분절 구간 수로 나 눈 평균적 기유도전류(    계산한 것과 같게 된다. 그 러므로 유도 구간의 각 전주 간 거리에 의한 분절 구간 마다의 유도전압을 계산하여 합산할 필요없이 구간 내
   I g 3 I g 2 I g 1 q p

    (2)에서 결과값은 식 (2)에 (9)를 도입 (1)에 Rate)을 5
(7) 1의
    (1)에서

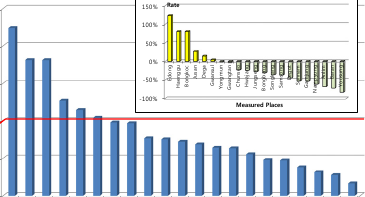
   그림 5의 분포를 표 그림 1의 것과 비교하여 (Over Rate)이 220%
1/5
   1100% 대비 전반적으로 100%

   (7)에서

   Rate)

   (8)이
6과
   -57%, -43%로서 14%
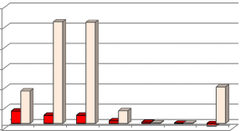
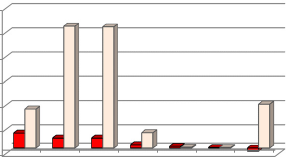
l ′ l ′ l ′ l 이와 같이 중성선 차폐계수를 유도 구간 위치에 따른 누설전류의 합성인 대지귀로전류 영향이 반영된 것으로 서 계산식을 도출한 것은 일반식 누설전류 요율 = V l ′ + V l ′ + V l ′ = 3 V l ′ 관계만에 의한 실무적 변형으로서 그 = j ω M l ′ ( I g 1 + I g 2 + I g 3 ) K 의한 것과 원리적으로 동일하다. 그러므로 식 하여 식 의한 기존 각 측정 개소의 유도전압을 계 = j ω M (3 l ′ ) ⎝ ⎜ ⎛ I g 1 + I 3 g 2 + I g 3 ⎞ ⎟ ⎠ K 와 산하여 같은 예측율(Estimation 분포를 보인다. 분석하여 보면 그림 = j ω M l ( I pq a ) K 단적 값에 의한 K 21 을 적용한 K: 식 차폐계수류를 통칭한 것 보면 가장 높은 과다 예측율 정도로서 기존 수 3.3.3 중성선 차폐계수 대체 계산식 준으로 줄어들었다. 또한, 예측율에 정의된 평균 기유도전류를 대지귀로전류 평균적으로 접근됨을 알 수 있다. 관점에서 일반적으로 다시 쓰면 식 된다. 과소 예측(Under 측면에서 기존 계산과 비교하 여 보면, 그림 같이 나타나고 K 21 에 대하여 계산을                적용한 개선이 개선 효과가 과소 예측율 증진되었다. 평균값으로써는 기존이                                       250% Estimation Rate Over/Under(8)
   200% 150%
s는
   100% 50 m라고
유도 구간 내 전주 간격에 의한 절분 구간 수 예를 들어 전주 간격이 하면 다음과 같 계산될 수 있다.50%0%          ←      Measured Places
   (8)에서

   (9)가

    (1)에서
그런데 이 식 유도전류의 원천이 되는 중성선 불평형전류 I n 에 대한 나머지 부분의 식을 분리시켜 쓰 되는데 이는 최초 유도전압 계산식 대응하는 의미를 갖게 된다는 것을 알 수 있고 곧 누설전류 효과가 반영된 중성선 차폐계수 계산식으로의 가능하다.90 7에Over RateMeasured Places
   -25%인데 이는 100% 25%이므로 350%보다는
과다 예측의 측면에서는 그림 비교된 것처 기존 과다 예측율에 비하면 현격하여 줄어든다는 것 보여주고 있다. 개소 삼송(Samsong)의 경우 과소율 예측에 대한 오차로서는 절대값인 기존의 과예측 훨씬 작은 범위 값이다.배전선에 의하여 통신선에 전자유도를 발생시키 전류를 계산할 때 실제 유도 구간의 위치에 따른 누 대지귀로전류의 영향이 반영되도록 매 전주 마다 발생하는 누설율만의 합성 관계로 표현된 실용적인 식을 전개하여 개발하였다. 이 식은 원래 기개발된 일반식에 직접 누설율들을 선대입하여 만들어졌으므로 결과값 동일하게 된다. 이렇게 식을 전개하였을 때 중성선 차 폐계수를 계산할 수 있는 식이 분리.도출된다. 이러한 누설전류의 영향이 반영된 계산식으로 처리하 측정 개소에 대한 비교 평가에서 알 수 있듯이 과소 부분에서는 증진 효과를 보이고, 특히 과
   14%의
Improve CurrentImprove Current측율을 거의 1/10 수준으로 감쇠시켜준다는 것을 알 수 있다. 개선된 방법에 의해서도 예측율 100%의 정확성을 갖 지 못하는 오차 범위의 부분은 단위 가공 배전선에 다른 위상의 회선이 복수로 설치되거나 병행되는 합성 영향의 문제가 있는데 이 부분의 계산 보완에 의한 정확도 향상 은 추가적인 연구가 필요한 상황이다. 91