http://dx.doi.org/10.5762/KAIS.2015.16.6.4131 ISSN 1975-4701 / eISSN 2288-4688
Journal of the Korea Academia-Industrial cooperation Society Vol. 16, No. 6 pp. 4131-4136, 2015
입사각에 따른 반사방지막 성능 개선에 관한 연구
Abstract
This paper compares and calculates more precisely the averaged reflectance of antireflection coating with different structure of single and 6 layer assuming the incident angle of light changing from 8 〬 to 60 〬 not like normal incidence as usual case. The reflectivity of AR coating of 6 layers with 180 nm thickness having index profile suggested as linear and quintic function and single layer with same thickness having even index are calculated and compared, when the wavelength of incident light ranges from 400 nm to 1200 nm. As the results the AR coating with 6 layers having quintic(linear) function index profile shows the lower reflectance about 11.6 %(14.6 %) than other index profiles, which is approximately 8 % lower reflectance compared with single layer case(about 19.6 %). This results could be applied for the better antireflection coating design applying to optical devices and filters. Key Words : Antireflection Coating, Transfer Matrix, Index Profile, Reflectivity
김창봉 1* 1 공주대학교 정보통신공학부 전파전공 The Study on the Improvement of Antireflection Coating Efficiency According to the Angle of Incidence Chang-Bong Kim 1* 1 Division of Radio-wave Engineering, Kongju National University 8 60 〬 까지 . 400 nm 1200 nm , 180 nm 1 5 분포를 갖는 6 180 nm 19.6 % 이고 , 6 %
요 약 본 논문은 반사방지막의 성능을 더 정확히 비교 및 분석하기 위하여 기존 방법과 달리 반사방지막에 수직입사가 아닌 입사각이 〬 에서 변화한다고 가정하고 단층 구조와 다층 구조의 반사방지막의 평균반사율을 계산하고 비교하 였다 입사파의 파장범위를 ∼ 라고 가정하고 분석에 사용된 반사방지막의 구조는 두께 인 차 및 차 함수의 굴절률 층 구조와 균일한 굴절률 분포를 갖는 단층구조이다 . 분석 결과로써 단층구조의 경우 평균반사율이 같은 두께의 층 구조의 1 차 함수 굴절률 분포에서는 14.2 % 이고 , 5 차 함수 경우에는 11.6 의 결과를 얻어 균일한 굴절률 분포의 단층구조 보다 5 차 함수 굴절률 분포를 갖는 6 층 구조의 경우 약 8% 의 반사율 감소 효과를 보았다 . 이러한 결과는 향후 광소자 및 광 필터에 적용되는 반사방지막 제작에 용용 될 수 있다고 판단된다 .
coating)
반사막의 반사방지의 정도를 결정하는 가장 중요한 요소 이다. 그리고 우수한 반사방지막을 얻기 위해서는 보다 반사방지막(Antireflection(AR) 기술은 광산 넓은 파장대에 걸쳐서 낮은 반사율을 얻는 기술이 중요 업에 다양하게 이용되고 있으며, 특히 광소자, 광 필터 하며 이를 구현하기 위하여 다층의 반사방지막 구조를 및 태양 전지 제작 공정 등에 광범위하게 적용되고 있다. 적용한다. 이때 다층의 반사방지막은 각 층의 두께 및 구 반사방지막은 기판 위에 얇은 투과막을 코팅하여 빛의 조를 적절하게 변화시키는 방법이 있고[1], 각층의 일정 간섭(Interference) 현상을 이용하여 반사를 방지한다. 반 한 두께 내에서 굴절률을 변화시키는 방법이 있다. 이 방 사방지막은 빛의 간섭현상을 이용하여 반사율을 제어하 법은 공기에서 기판 방향으로 굴절률을 증가하는 방식이 므로 기판위에 증착되는 코팅물질의 굴절률 및 두께가 며, 이때 굴절률의 변화는 또는 고차함수 등으로 굴1차, 4131 하게 된 것은 실리콘 나노막대 구조를 갖는 방식을 사용 율을 계산하고 비교한다. 굴절률 분포를 단순화하기 위 하고 나노막대의 각도를 변화시키어 정밀한 굴절률 제어 하여 반사방지막의 총 두께 로 가정하고, 1차, (1.09 ∼ 2.6)가 가능하게 하거나, 원자층증착법(Atomic 5차 함수 굴절률 분포인 경우 굴절률은 기판 쪽으로 갈 Layer Deposition)[3]을 사용하여 굴절률이 서로 다른 수록 증가한다고 가정한다. 이때 적용된 굴절률 분포 중 물질을 혼합하여 정밀한 굴절률 제어(1.7 ∼ 2.42)가 가 1차 분포는 능하기 때문이다. 기존의 원자증착법등의 연구에서는 반 사방지막에 수직으로 빛이 입사하는 가정 하에 반사방지 ≤ ≤ 본 논문은 2013년 공주대학교 학술연구지원사업의 연구비지원에 의하여 연구되었음. * Corresponding Author : Chang-Bong Kim(Kongju National Univ.) Tel: +82-41-521-9193 email: Received February 13, 2015 Revised (1st May 8, 2015, 2nd May 20, 2015) Accepted June 11, 2015 Published June 30, 2015는 보다 일반적인 경우로서 반사방지막에 진행하는 빛이 이고, 임의의 입사각을 갖을 때 단층 및 다층 구조의 서로 다 른 굴절률 분포를 갖는 반사방지막에 대하여 반사율을 5차 분포는 비교 및 분석하였다. , ≤ ≤
(2)
6층 AR
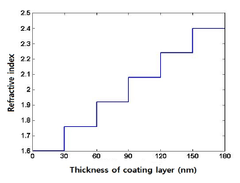
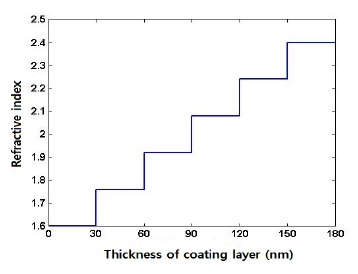
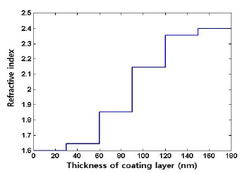
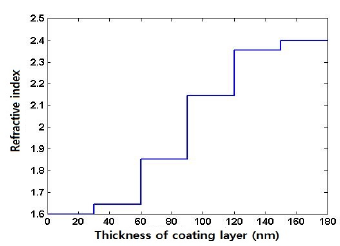
2와 3은 (1)과 (2)를 두께 180 nm의 6층 분포(1차 및 5차 함수)를 나타낸다.
6개의
1과 같이 이루진다. AR 30 nm 180 nm로
,
, ... 1은 6층
, ,
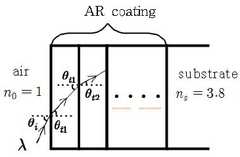
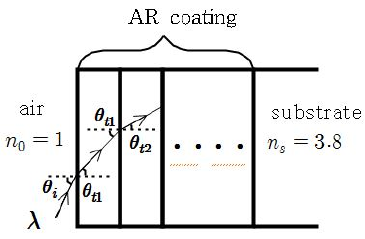
이다. 이때 는 구조 중 첫 번째 층의 굴절률이고 2.1 반사방지막의 구조 및 굴절률 분포 는 여섯 번째 층의 굴절률을 나타낸다. 아래의 그림 분석하고자 하는 코팅구조는 아래의 그림 식 구조에 적용 기판 위의 다층의 코팅 영역으로 코 한 굴절률 팅은 층으로 이루어지며 각층의 두께는 이 고 코팅의 전체 두께는 가정한다. 빛이 입사 각 로 코팅표면에 입사할 때 각층의 투과각을 각각 이고, 기판에서의 투과각을 라고 가 정한다. 이때 왼쪽 매질부터 영역 공기 )이고, 구조의 반사방지막의 굴절률은 각 각 ... 등 으로 표시하고, 기판의 굴절률은 이라고 가정 한다.본 연구에서는 반사방지막이 6층 구조의 Southwell 4132 (6)은 2.1 절에서 제시된 6층(1차, 5차 함수의 굴절률 분포) 인 및 단층(균일한 굴절률 분포)구조의 반사율을 비교 및 계산하고자 층 코팅매질에서의 한다. 우선 반사율을 다층 구조를 결정하는 해석하기 전달매트릭스에 위해서 단 대한 이론이 필요하다. 단층 코팅 매질에 입사되는 빛이 임의의 입사각 일 때 TE(Transverse electric) 및 로 됨을 알 수 있다. TM(Transverse magnetic) 경우에 따라 틀려지는 전달매 2.2.2 굴절률 분포에 따른 반사율 트릭스 는 다음과 같이 주어진다[6]. 1) 파장 변화에 따른 반사율 1 0.9 0.8 0.7 (TE (TM
(3) 여기에서 경우) 이다. 이며, 이때 경우) 은 코팅매질의 Reflectivity 0.4 0.3 0.1 0.2 0.5 0.6 굴절률, 은 코팅매질에서의 투과각, 는 입사파의 400 0 자유공간상의 파장, 는 코팅매질의 두께이다. 여기에 서 코팅매질에서의 투과각 은 Snell의 법칙에 따라 1 (4) 0.9 0.8 0.7 로 주어지고 입사되는 매질은 공기이며 굴절률 0.6 라고 가정한다. 만약 코팅이 N-다층의 구조를 갖는다면, Reflectivity 0.5 0.4 ∙∙∙ (5) 0.3 0.2 0.1 로 주어지고, ∙∙∙ 은 각 코팅 층에 0 400 대한 전달 매트릭스이다. 이때 다층구조의 반사율 은
기존의 연구에서는 반사율 계산을 단순화하기 위하여 (6) 광원의 빛이 수직입사 한다고 가정하였으나, 본 연구에 서는 파장을 까지 변화시킬 수 있 로 주어지며 는 코팅층에서 기판으로의 투과각이고, 는 광원(예를 들면 파장가변 레이저 등)의 빛이 임의의 는 기판의 굴절률이다. 만약 빛이 입사각 , 입사각으로 반사방지막에 입사 된다고 할 때 반사율을4133
(7)
single layer linear (6 layers) quintic (6 layers) 500 600 700 800 900 1000 1100 1200 Wavelength(nm)
single layer linear (6 layers) quintic (6 layers) 500 600 700 800 900 1000 1100 1200 Wavelength(nm)
400 nm에서 1200 nm
TE와 TM의
하며, 6층 구조일 때의 굴절률 분포는 5차 함수의 분포를 갖는다고 빛은 TE 와 TM 성분의 경우 지는데, 아래 그림 4는 입사각 고정했을 때의 TE 경우 그림 4와 5의 결과를 보면 TE의 5차 함수, 1차 함수, 단층 순으로
6과 7은 TM
TE경
8은 400 nm ~ 1200 nm
TM 경우 으로 5차
0.6 Reflectivity 0.5 0.4
50 %
그림 2와 3의 1차 사각에 따른 평균 반사율 값을 단층, 다층 구조의 반사방 및 가정한다. 이때 입사되 지막에서 구하고자 한다. 앞의 결과에서 보듯이 주어진 는 각각의 반사율이 틀려 파장대에서 입사각이 존재할 경우 입사각의 크기에 관계 가 로 그림 5는 없이 평균적으로 단층, 1차 함수 및 5차 함수 순으로 반 로 반사율 값을 나타낸다. 사율이 적어지는 것을 볼 수 있었다. 따라서 본 절에서는 경우 입사각이 증가해 경우 임의의 입사각, 즉 도 반사율이 적어지는 일 때의 반사율 값의 평균치를 계산하여 것을 알 수 있다. 마찬가지로 그림 경우 입 단층, 1차 함수, 5차 함수 각각의 경우 반사율을 비교하 사각 가 와 일 때 반사율을 나타낸다. 고자 한다. 여기에서 반사방지막의 성능은 반사율이 클 우와 비슷하게 5차 함수, 1차 함수, 단층 순으로 전반적 수록 낮아지는 반비례 관계이다. 그리고 입사하는 광원 으로 반사율이 적어지는 것을 알 수 있다. 즉, 주어진 파 의 빛은 일반적인 경우인 무편광 상태라고 가정한다. 그 장대에서 입사각이 있을 경우에도 입사각의 크기에 관계 림 파장에서 입사각에 따른 반 없이 TE 와 TM 두 경우에 대체적으로 단층, 1차 함수, 사율을 보여준다.(TE의 경우) 전반적으로 5차 함수, 1차 5차 함수 순으로 평균적인 반사율이 적어진다는 것을 알 함수, 단층 순으로 낮은 반사율을 보이고 있다. 그림 9 수 있다. 는 입사각에 따른 반사율을 보여준다. 평균적 1 함수, 1차 함수, 단층 순으로 낮은 반사율을 보 0.9 이고 있다. 그러나 약 이하의 입사각에서는 5차 와 0.8 1차 함수의 반사율 차이가 크지 않고, 이상의 입사 0.7 각에서는 5차 함수, 1차 함수, 단층의 반사율의 크기가 바뀌는 다른 결과를 보여준다. 일반적으로 무편광 된 광 single layer 원은 TE 와 TM 성분이 각각 라고 가정 할 수 있 linear (6 layers) 고[7], 그림 10은 무편광 된 광원의 빛이 입사할 때 입사 0.3 quintic (6 layers) 각 변화에 따른 반사율을 나타낸다. 그림 10으로부터 반 0.2 0.1 사방지막의 성능을 비교하기 위해서 각각의 굴절률 분포 0 에 따른 반사율 값의 평균을 % 로 구하면 표 1과 같다. 400 500 600 700 800 900 1000 1100 1200 Wavelength(nm)
1 0.25 0.9 single layer 0.2 0.8 0.6 0.7 single layer Reflectivity 0.15 linear (6 layers) Reflectivity 0.5 quintic (6 layers) linear (6 layers) 0.1 0.4 0.05 0.3 quintic (6 layers) 0.2 0 0 10 20 30 40 50 60 0.1 Incident angle(deg)
1000 1100 1200
0 400 500 600 700 800 900 Wavelength(nm)(TE case)4134 1차
14.2 %
6층 5차 6층
분포에서는 11.6 % 5차 함수
sinle layer 0.2 Reflectivity 0.15 linear (6 layers) quintic (6 layers) 0.18 %0.05이고, 같은 두께의 구조의 함수 굴절률 분포에 서는 이고, 함수 굴절률 를 얻었다. 따라서 단층 구조 보다 구조의 굴절률 분포가 약 의 반사율 감소 효과를 보았다. 이러한 결과는 향후 광소자 및 광필터에 적용되는 반사 방지막 제작에 활용 될 수 있다고 판단된다.0 0 10 20 30 40 50 60 Incident angle(deg)
400 nm
1200 nm의
[1] A. Mouldi and M. Kanzari, “Broad Multilayer Antireflection Coating by Apodized and Chirped Photonic Crystal", Optics Communications, vol. 284, pp. 0.25 4124-4128, Aug., 2011. single layer 0.2 DOI: http://dx.doi.org/10.1016/j.optcom.2011.05.005 Reflectivity 0.15 linear (6 layers) [2] S.Y. Efficiency issues Lee in Journal and in Silicon J.W. of IITP, Lim, Thin-Film no.1488, "Improvement Solar pp. 1-13, Cell", Mar., of Current Optical 2011. 0.1 [3] J. W. Lim, S. H. Lee, J. K. Kim, and S. J. Yun, 0.05 “Antireflection Properties of Al 2 O 3 and Al x Ti 1-x O y Films quintic (6 layers) on ZnO:Ga Coated Si Wafer for Thin-Film Solar Cell", 0 0 10 20 30 40 50 60 Electrochemical and Solid-State Letters, vol. 13, G17, Incident angle(deg) Aug., 2010. DOI: http://dx.doi.org/10.1149/1.3269612 (1/2*(TE+TM) case) [4] W.H. Southwell, “Gradient-index Antireflection Coatings", Optics Letters, vol. 8, no. 11, pp. 584-586, Nov., 1983. DOI: http://dx.doi.org/10.1364/OL.8.000584 C. B. Kim, "The Study on the Antireflection Coating Design Scheme According to the Index Profile in the Thin-Film silicon Solar Cell", Journal of The Korea Academia-Industrial cooperation Society, vol. 13, no. 9, pp. 4139-4145, Sept,, 2012. DOI: http://dx.doi.org/10.5762/KAIS.2012.13.9.4139 Filiz Karaomeriloglu, "Reflectance Profile of BaTiO3 on Multilayer Antireflection Coating Systems", The Japan Society of Applied Physics,, vol. 50, pp. 기존의 원자증착법등의 연구에서는 반사방지막에 수 05FH05-05FH06, May, 2011. 직으로 빛이 입사하는 가정 하에 반사방지막의 성능 분 DOI: http://dx.doi.org/10.1143/JJAP.50.05FH05 석이 이루어 졌으나 본 연구에서는 보다 실제의 일반적 [7] Frank L. Pedrotti, S.J., L. M. Pedrotti, L.S. Pedrotti, 인 경우로서 입사각 ∼ 범위에서 ∼ "Introduction to Optics", pp. 476-481, Pearson 무편광 빛이 입사한다고 가정하였다. 이때 International Edition, Publication, 3r d edition, 2007. 서로 다른 굴절률 분포를 갖는 단층 과 구조의 반사6층 4135
• 1988년 6월 : Florida Institute of Technology 전기전자공학 (공학석사) • 1992년 5월 : Texas A&M University 전기전자공학 (공학박사) • 2000년 9월 ~ 현재 : 국제전기전 자공학회 (IEEE) Senior Member 1993년 3월 ~ 현재 : 공주대학교
• 전파전공 정교수
<관심분야> 광소자, 광센서, 태양전지 반사막 설계기술
4136
1. 서론
coating)
반사막의 반사방지의 정도를 결정하는 가장 중요한 요소 이다. 그리고 우수한 반사방지막을 얻기 위해서는 보다 반사방지막(Antireflection(AR) 기술은 광산 넓은 파장대에 걸쳐서 낮은 반사율을 얻는 기술이 중요 업에 다양하게 이용되고 있으며, 특히 광소자, 광 필터 하며 이를 구현하기 위하여 다층의 반사방지막 구조를 및 태양 전지 제작 공정 등에 광범위하게 적용되고 있다. 적용한다. 이때 다층의 반사방지막은 각 층의 두께 및 구 반사방지막은 기판 위에 얇은 투과막을 코팅하여 빛의 조를 적절하게 변화시키는 방법이 있고[1], 각층의 일정 간섭(Interference) 현상을 이용하여 반사를 방지한다. 반 한 두께 내에서 굴절률을 변화시키는 방법이 있다. 이 방 사방지막은 빛의 간섭현상을 이용하여 반사율을 제어하 법은 공기에서 기판 방향으로 굴절률을 증가하는 방식이 므로 기판위에 증착되는 코팅물질의 굴절률 및 두께가 며, 이때 굴절률의 변화는 또는 고차함수 등으로 굴1차, 4131 하게 된 것은 실리콘 나노막대 구조를 갖는 방식을 사용 율을 계산하고 비교한다. 굴절률 분포를 단순화하기 위 하고 나노막대의 각도를 변화시키어 정밀한 굴절률 제어 하여 반사방지막의 총 두께 로 가정하고, 1차, (1.09 ∼ 2.6)가 가능하게 하거나, 원자층증착법(Atomic 5차 함수 굴절률 분포인 경우 굴절률은 기판 쪽으로 갈 Layer Deposition)[3]을 사용하여 굴절률이 서로 다른 수록 증가한다고 가정한다. 이때 적용된 굴절률 분포 중 물질을 혼합하여 정밀한 굴절률 제어(1.7 ∼ 2.42)가 가 1차 분포는 능하기 때문이다. 기존의 원자증착법등의 연구에서는 반 사방지막에 수직으로 빛이 입사하는 가정 하에 반사방지 ≤ ≤ 본 논문은 2013년 공주대학교 학술연구지원사업의 연구비지원에 의하여 연구되었음. * Corresponding Author : Chang-Bong Kim(Kongju National Univ.) Tel: +82-41-521-9193 email: Received February 13, 2015 Revised (1st May 8, 2015, 2nd May 20, 2015) Accepted June 11, 2015 Published June 30, 2015는 보다 일반적인 경우로서 반사방지막에 진행하는 빛이 이고, 임의의 입사각을 갖을 때 단층 및 다층 구조의 서로 다 른 굴절률 분포를 갖는 반사방지막에 대하여 반사율을 5차 분포는 비교 및 분석하였다. , ≤ ≤
(2)
2. 굴절률 분포에 따른 반사율
2와 3은 (1)과 (2)를 두께 180 nm의 6층 분포(1차 및 5차 함수)를 나타낸다.
6개의
1과 같이 이루진다. AR 30 nm 180 nm로
,
, ... 1은 6층
, ,
이다. 이때 는 구조 중 첫 번째 층의 굴절률이고 2.1 반사방지막의 구조 및 굴절률 분포 는 여섯 번째 층의 굴절률을 나타낸다. 아래의 그림 분석하고자 하는 코팅구조는 아래의 그림 식 구조에 적용 기판 위의 다층의 코팅 영역으로 코 한 굴절률 팅은 층으로 이루어지며 각층의 두께는 이 고 코팅의 전체 두께는 가정한다. 빛이 입사 각 로 코팅표면에 입사할 때 각층의 투과각을 각각 이고, 기판에서의 투과각을 라고 가 정한다. 이때 왼쪽 매질부터 영역 공기 )이고, 구조의 반사방지막의 굴절률은 각 각 ... 등 으로 표시하고, 기판의 굴절률은 이라고 가정 한다.본 연구에서는 반사방지막이 6층 구조의 Southwell 4132 (6)은 2.1 절에서 제시된 6층(1차, 5차 함수의 굴절률 분포) 인 및 단층(균일한 굴절률 분포)구조의 반사율을 비교 및 계산하고자 층 코팅매질에서의 한다. 우선 반사율을 다층 구조를 결정하는 해석하기 전달매트릭스에 위해서 단 대한 이론이 필요하다. 단층 코팅 매질에 입사되는 빛이 임의의 입사각 일 때 TE(Transverse electric) 및 로 됨을 알 수 있다. TM(Transverse magnetic) 경우에 따라 틀려지는 전달매 2.2.2 굴절률 분포에 따른 반사율 트릭스 는 다음과 같이 주어진다[6]. 1) 파장 변화에 따른 반사율 1 0.9 0.8 0.7 (TE (TM
(3) 여기에서 경우) 이다. 이며, 이때 경우) 은 코팅매질의 Reflectivity 0.4 0.3 0.1 0.2 0.5 0.6 굴절률, 은 코팅매질에서의 투과각, 는 입사파의 400 0 자유공간상의 파장, 는 코팅매질의 두께이다. 여기에 서 코팅매질에서의 투과각 은 Snell의 법칙에 따라 1 (4) 0.9 0.8 0.7 로 주어지고 입사되는 매질은 공기이며 굴절률 0.6 라고 가정한다. 만약 코팅이 N-다층의 구조를 갖는다면, Reflectivity 0.5 0.4 ∙∙∙ (5) 0.3 0.2 0.1 로 주어지고, ∙∙∙ 은 각 코팅 층에 0 400 대한 전달 매트릭스이다. 이때 다층구조의 반사율 은
기존의 연구에서는 반사율 계산을 단순화하기 위하여 (6) 광원의 빛이 수직입사 한다고 가정하였으나, 본 연구에 서는 파장을 까지 변화시킬 수 있 로 주어지며 는 코팅층에서 기판으로의 투과각이고, 는 광원(예를 들면 파장가변 레이저 등)의 빛이 임의의 는 기판의 굴절률이다. 만약 빛이 입사각 , 입사각으로 반사방지막에 입사 된다고 할 때 반사율을4133
(7)
single layer linear (6 layers) quintic (6 layers) 500 600 700 800 900 1000 1100 1200 Wavelength(nm)
single layer linear (6 layers) quintic (6 layers) 500 600 700 800 900 1000 1100 1200 Wavelength(nm)
400 nm에서 1200 nm
TE와 TM의
하며, 6층 구조일 때의 굴절률 분포는 5차 함수의 분포를 갖는다고 빛은 TE 와 TM 성분의 경우 지는데, 아래 그림 4는 입사각 고정했을 때의 TE 경우 그림 4와 5의 결과를 보면 TE의 5차 함수, 1차 함수, 단층 순으로
6과 7은 TM
TE경
8은 400 nm ~ 1200 nm
TM 경우 으로 5차
0.6 Reflectivity 0.5 0.4
50 %
그림 2와 3의 1차 사각에 따른 평균 반사율 값을 단층, 다층 구조의 반사방 및 가정한다. 이때 입사되 지막에서 구하고자 한다. 앞의 결과에서 보듯이 주어진 는 각각의 반사율이 틀려 파장대에서 입사각이 존재할 경우 입사각의 크기에 관계 가 로 그림 5는 없이 평균적으로 단층, 1차 함수 및 5차 함수 순으로 반 로 반사율 값을 나타낸다. 사율이 적어지는 것을 볼 수 있었다. 따라서 본 절에서는 경우 입사각이 증가해 경우 임의의 입사각, 즉 도 반사율이 적어지는 일 때의 반사율 값의 평균치를 계산하여 것을 알 수 있다. 마찬가지로 그림 경우 입 단층, 1차 함수, 5차 함수 각각의 경우 반사율을 비교하 사각 가 와 일 때 반사율을 나타낸다. 고자 한다. 여기에서 반사방지막의 성능은 반사율이 클 우와 비슷하게 5차 함수, 1차 함수, 단층 순으로 전반적 수록 낮아지는 반비례 관계이다. 그리고 입사하는 광원 으로 반사율이 적어지는 것을 알 수 있다. 즉, 주어진 파 의 빛은 일반적인 경우인 무편광 상태라고 가정한다. 그 장대에서 입사각이 있을 경우에도 입사각의 크기에 관계 림 파장에서 입사각에 따른 반 없이 TE 와 TM 두 경우에 대체적으로 단층, 1차 함수, 사율을 보여준다.(TE의 경우) 전반적으로 5차 함수, 1차 5차 함수 순으로 평균적인 반사율이 적어진다는 것을 알 함수, 단층 순으로 낮은 반사율을 보이고 있다. 그림 9 수 있다. 는 입사각에 따른 반사율을 보여준다. 평균적 1 함수, 1차 함수, 단층 순으로 낮은 반사율을 보 0.9 이고 있다. 그러나 약 이하의 입사각에서는 5차 와 0.8 1차 함수의 반사율 차이가 크지 않고, 이상의 입사 0.7 각에서는 5차 함수, 1차 함수, 단층의 반사율의 크기가 바뀌는 다른 결과를 보여준다. 일반적으로 무편광 된 광 single layer 원은 TE 와 TM 성분이 각각 라고 가정 할 수 있 linear (6 layers) 고[7], 그림 10은 무편광 된 광원의 빛이 입사할 때 입사 0.3 quintic (6 layers) 각 변화에 따른 반사율을 나타낸다. 그림 10으로부터 반 0.2 0.1 사방지막의 성능을 비교하기 위해서 각각의 굴절률 분포 0 에 따른 반사율 값의 평균을 % 로 구하면 표 1과 같다. 400 500 600 700 800 900 1000 1100 1200 Wavelength(nm)
1 0.25 0.9 single layer 0.2 0.8 0.6 0.7 single layer Reflectivity 0.15 linear (6 layers) Reflectivity 0.5 quintic (6 layers) linear (6 layers) 0.1 0.4 0.05 0.3 quintic (6 layers) 0.2 0 0 10 20 30 40 50 60 0.1 Incident angle(deg)
1000 1100 1200
0 400 500 600 700 800 900 Wavelength(nm)(TE case)4134 1차
14.2 %
6층 5차 6층
분포에서는 11.6 % 5차 함수
sinle layer 0.2 Reflectivity 0.15 linear (6 layers) quintic (6 layers) 0.18 %0.05이고, 같은 두께의 구조의 함수 굴절률 분포에 서는 이고, 함수 굴절률 를 얻었다. 따라서 단층 구조 보다 구조의 굴절률 분포가 약 의 반사율 감소 효과를 보았다. 이러한 결과는 향후 광소자 및 광필터에 적용되는 반사 방지막 제작에 활용 될 수 있다고 판단된다.0 0 10 20 30 40 50 60 Incident angle(deg)
References
3. 결론
400 nm
1200 nm의
[1] A. Mouldi and M. Kanzari, “Broad Multilayer Antireflection Coating by Apodized and Chirped Photonic Crystal", Optics Communications, vol. 284, pp. 0.25 4124-4128, Aug., 2011. single layer 0.2 DOI: http://dx.doi.org/10.1016/j.optcom.2011.05.005 Reflectivity 0.15 linear (6 layers) [2] S.Y. Efficiency issues Lee in Journal and in Silicon J.W. of IITP, Lim, Thin-Film no.1488, "Improvement Solar pp. 1-13, Cell", Mar., of Current Optical 2011. 0.1 [3] J. W. Lim, S. H. Lee, J. K. Kim, and S. J. Yun, 0.05 “Antireflection Properties of Al 2 O 3 and Al x Ti 1-x O y Films quintic (6 layers) on ZnO:Ga Coated Si Wafer for Thin-Film Solar Cell", 0 0 10 20 30 40 50 60 Electrochemical and Solid-State Letters, vol. 13, G17, Incident angle(deg) Aug., 2010. DOI: http://dx.doi.org/10.1149/1.3269612 (1/2*(TE+TM) case) [4] W.H. Southwell, “Gradient-index Antireflection Coatings", Optics Letters, vol. 8, no. 11, pp. 584-586, Nov., 1983. DOI: http://dx.doi.org/10.1364/OL.8.000584 C. B. Kim, "The Study on the Antireflection Coating Design Scheme According to the Index Profile in the Thin-Film silicon Solar Cell", Journal of The Korea Academia-Industrial cooperation Society, vol. 13, no. 9, pp. 4139-4145, Sept,, 2012. DOI: http://dx.doi.org/10.5762/KAIS.2012.13.9.4139 Filiz Karaomeriloglu, "Reflectance Profile of BaTiO3 on Multilayer Antireflection Coating Systems", The Japan Society of Applied Physics,, vol. 50, pp. 기존의 원자증착법등의 연구에서는 반사방지막에 수 05FH05-05FH06, May, 2011. 직으로 빛이 입사하는 가정 하에 반사방지막의 성능 분 DOI: http://dx.doi.org/10.1143/JJAP.50.05FH05 석이 이루어 졌으나 본 연구에서는 보다 실제의 일반적 [7] Frank L. Pedrotti, S.J., L. M. Pedrotti, L.S. Pedrotti, 인 경우로서 입사각 ∼ 범위에서 ∼ "Introduction to Optics", pp. 476-481, Pearson 무편광 빛이 입사한다고 가정하였다. 이때 International Edition, Publication, 3r d edition, 2007. 서로 다른 굴절률 분포를 갖는 단층 과 구조의 반사6층 4135
• 1988년 6월 : Florida Institute of Technology 전기전자공학 (공학석사) • 1992년 5월 : Texas A&M University 전기전자공학 (공학박사) • 2000년 9월 ~ 현재 : 국제전기전 자공학회 (IEEE) Senior Member 1993년 3월 ~ 현재 : 공주대학교
• 전파전공 정교수
<관심분야> 광소자, 광센서, 태양전지 반사막 설계기술
4136