http://dx.doi.org/10.5762/KAIS.2015.16.3.1630 ISSN 1975-4701 / eISSN 2288-4688
Journal of the Korea Academia-Industrial cooperation Society Vol. 16, No. 3 pp. 1630-1638, 2015
반응표면법과 크리깅의 혼합모델을 이용한 구조설계방법
Nam-Hee Kim1, Kwon-Hee Lee
Abstract
The finite element analysis has become an essential process to investigate the structural performance in many industry fields. In addition, the computer's performance is improving rapidly, but in large design problems, there is a limit to apply the optimal design techniques. For this, it is general to introduce a metamodel based optimization technique. The method to generate an approximate model can be classified into curve fitting and interpolation, and each representative one is response surface model and kriging interpolation method. This study proposes an ensemble model made of RSM and kriging to solve a structural design problem. The suggested method is applied to the designs of two bar and automobile outer tie rod. Key Words : Ensemble Model, Interpolation Method, Kriging, Outer Tie Rod, RSM(Response Surface Method), Structural Design
김남희 1 , 이권희 1* 1 동아대학교 기계공학과 A Structural Design Method Using Ensemble Model of RSM and Kriging
요 약 많은 산업분야에서 구조설계 시 구조성능을 검토하기 위한 유한요소해석은 필수적인 과정이 되었다. 이와 함께, 컴퓨 터의 성능도 급속도로 개선되고 있지만 대형 문제의 경우에는 최적설계기법을 적용하는데 한계가 있다. 이러한 대형 문제의 최적화를 위하여 메타모델을 이용한 근사모델을 이용하고 있다. 근사모델을 생성하는 방법은 곡선맞춤법과 내삽법으로 분류 할 수 있는데, 반응표면모델과 크리깅 모델이 대표적인 것이다. 그러나 각 모델은 오버피팅이나 언더피팅이 될 수 있는 단점 이 있다. 본 연구에서는 반응표면과 크리깅으로 구성되는 혼합모델에 의한 메타모델을 이용하여 구조설계에 적용하고자 한 다. 제안된 방법을 2부재 구조물과 자동차용 아우터타이로드의 구조설계에 적용하였다.
1. 서론
화문제로 대치하게 되면 최적해를 산출하기 위해 기존의 경사도기반최적화 알고리듬(gradient based optimization algorithm)이나 심지어 함수계산이 많이 요구되는 유전 자알고리듬, 시뮬레이티드어닐링 등의 통계적 최적화 알 고리듬을 사용할 수도 있다[3]. 이러한 메타모델을 이용한 최적설계 방법의 장점으로 인해 상용프로그램인 ANSYS[4], LS-OPT[5], PAM-OPT[6], PiANO[7], VisualDOC[8], iSIGHT[9] 등에서도 메타모 델을 이용한 최적화 모듈을 제공하고 있다. 메타모델을 생성하는 방법으로는 반응표면법, 크리깅 내삽법, 뉴럴네크워크 알고리듬 등이 있다. 이러한 메타 모델은 모두 각 근사모델과 실제 반응값의 평균제곱오차 (mean square error)를 최소화함으로서 각 모델의 파라 미터를 추정하여 근사모델을 결정한다. 최근에는 최적화 를 위해 단일 메타모델이 아닌 2개 이상의 메타모델이 혼 합된 혼합메타모델(ensemble model, hybrid model, mutiple surrogate)[10~13]을 이용하기도 한다. 본 연구에서는 반응표면법과 크리깅내삽법으로 구성 된 혼합메타모델을 구성하고 이를 구조설계에 적용하고 자 한다. 혼합메타모델은 가중치가 고려된 다중목적함수 를 이용하였고 가중치는 교차검증(CV, cross validation) 값을 이용하여 결정된다. 개발된 프로그램에서 이 값은 k-평균 클러스터(k-means cluster)를 이용하여 계산할 수 도 있고 설계자가 직접 입력할 수도 있게 하였다. 이 부재설계(two-bar design)문제[1, 14]와 승용차용 아우터 타이로드의 형상설계문제[15, 16]를 적용대상으로 하여 개발된 프로그램의 유용성을 검증하였다.
2. 메타모델의 종류 및 특징
반응표면법은 가장 고전적인 메타모델을 생성하는 방 법으로서 미리 가정한 다항식의 계수를 결정하는 곡선맞 춤의 한 방법이다. 또한 크리깅방법은 한 쌍의 설계점에 대한 상관성을 상관행렬(correlation matrix)로 구성하고 이에 대한 파리미터를 결정하는 내삽법의 하나이다. 반 면에 뉴럴네트워크는 그 종류가 다양한데 오차역전파알 고리듬(back propagation algorithm), 레이디얼베이시스 함수(radial basis function) 방법 등이 있는 내삽법의 일 종이다. 구조최적설계에 자주 사용하는 레이디얼베이시스함
모델 생성 이전에 가정해야 하는 값들이 있다. 은닉층 (hidden layer)의 개수, 은닉층의 뉴런 개수, 클러스터 개 수, 클러스터링 방법 등이 그것이다. 메타모델 생성 시 이 러한 자유도는 번거로운 과정이지만 신뢰도 높은 메타모 델을 생성할 수 있는 장점이 될 수도 있다. 그러나 이 점 이 혼합메타모델을 이용한 최적설계 자동화 프로그램에 장애가 되었다. 따라서 본 연구에서는 곡선맞춤법의 대 표로 반응표면모델을, 내삽법의 대표로 크리깅밥법을 선 정하여 혼합메타모델을 구성하였다. 다음은 각 메타모델 에 대한 간략한 설명이다. 2.1 반응표면법 반응표면법은 변수와 반응치와의 관계를 규명해내는 방법으로서 Box와 Wilson[17]이 1950년대에 제안하였다. 그 이후 최적설계 연구자들은 반응치를 반응표면모델로 대치하여 최적설계 문제를 단순화 시키고자 하였다. 구 조설계문제에 반응표면법을 이용할 경우 주로 다항식을 이차함수로 가정한다. 변수 n개에 대하여 다항식은 다음 과 같이 가정한다.
여기서 x i( i=1,..,n)는 설계변수, y는 반응치, β i 는 다항식의 계수를 의미한다. 표본점 m개에 대해 식 (1)을 행렬방정 식으로 표현하면 다음과 같이 된다.
여기서 β는 다음과 같이 결정된다.
구조최적설계의 경우 주로 고려되는 반응치는 중량, 변위, 응력, 고유진동수 등이 있는데, 설계변수에 대한 비 선형성이 크지 않고 행렬 X의 크기를 최소로 하기 위해 2차함수로 근사화 시키는 것이 일반적이다. 그러나 3차 함수로 가정하는 것이 보다 정확하며 다음절에 소개되는 크리깅과의 신뢰도 비교를 고려하면 반응표면모델로서 2
인 경우 반응표면모델을 2차함수, 3차함수로 가정했을 때 행렬 X의 크기 p×p의 p는 각각 다음과 같다. p = 1 + 2 n + n ( n − 1 ) for sec ond order 2 p = 1 + 2 n + n ( n 2 − 1 ) + n 2 for third order (4) 본 연구에서는 3차 반응표면모델을 이용하였다. 식 (3)이 구해지면 다음 식을 이용하여 반응치를 예측할 수 있다. ^ y ( x ) = [ 1 x 1 ...... x n ... x 1 x 2 ..... x n 3 ] β (5) 추정된 반응표면모델의 신뢰도를 평가할 수 있는 한 방법으로 R 2 와 수정 R 2adj 가 있다. 이 값들은 표본점에서 의 반응값들이 반응표면모델로 표현되는 정도를 수치화 한 것이다. 이 값은 1에 가까워야 하고 경험적으로 최적 화를 위해서는 0.95이상의 값을 가져야 한다. 그러나 이 값들이 임의의 설계점에서 예측된 반응치값의 정확도를 의미하는 것은 아니다. 2.2 크리깅내삽법 성능함수 y(x)의 근사화모델은 다음과 같이 표시될 수 있다. y ( x ) = b + z ( x ) (6) 여기서 b는 상수, z(x)는 평균이 0이고 분산이 σ 2 인 정규 분포를 따르는 확률변수이다. y(x)와 크리깅모델의 평균 제곱오차가 최소가 되도록 하면 크리깅모델은 다음과 같 이 구해진다. ∧ ∧ ∧ y ( x ) = b + r T ( x ) R − 1 ( y − β i ) (7) 여기서 ^는 추정치를 의미하며 는 β의 추정치, R -1 은 상관행렬 R의 역행렬, r은 상관벡터, i는 표본점 m개 성 분을 갖는 단위벡터이다. 상관행렬에는 파라미터 θ i (i=1,..,n)가 있는데 이는 다 음의 최적화문제를 해결해야 구할 수 있다. ∧ [ m ⋅ ln ( σ 2 ) + ln R ] maximize −
(8)
여기서θ i >0이다. 본 연구에서는 이 정식화를 해결하기 위하여 SUMT(sequential unconstrained minimization technique)를 이용하였다.
3. 혼합메타모델과 최적설계과정
3.1 다중목적함수 기존의 연구[10∼13]에서는 혼합메타모델을 위하여 다음과 같은 다중목적함수를 제안하여 이용하고 있다.
여기서 c는 메타모델의 개수, w i 는 가중치를 의미한다. 본 연구에서는 반응표면 모델과 크리깅의 메타모델을 이용 하므로 c는 2이다. 그리고 y 1 (x)은 반응표면모델을, y 2 (x) 는 크리깅모델을 의미한다. 비선형성이 큰 구조성능의 반응치를 반응표면모델로 대치할 경우, 언더피팅(under-fitting)이 될 수 있다. 반면 에 비선형성이 크지 않은 구조성능의 반응치를 크리깅모 델로 대치할 경우 국부적으로 오버피팅(over-fitting)이 될 가능성이 있다. 식 (9)로 정의되는 다중목적함수를 이 용하여 메타모델을 구성하면 위와 같은 언더피팅과 오버 피팅의 문제점을 해결할 수 있다. 3.2 가중치의 결정 기존의 연구중 Zerpa[10]는 반응표면모델, 크리깅모 델, 레이디얼베이시스 함수로 예측되는 각 반응치의 분 산을 이용하여 가중치를 정의하였다. 또한 Acar[11], Viana[12], Yin[13] 등은 각 모델을 생성 후, 교차검증 (CV, cross validation)값에 의해 구해지는 오차를 이용하 여 가중치를 계산하였다. 본 연구에서는 후자를 이용하 였으며 선택적으로 사용자가 가중치를 결정 할 수 있게 하였다. 메타모델의 교차검증값 CV는 다음과 같다.
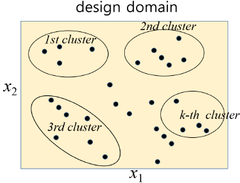
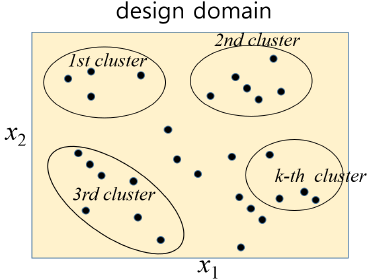
[Fig. 1] k-means clustering ^ 여기서 y − i 는 m개의 표본점중 i 번째 설계점을 제외하 고 생성된 메타모델을 의미한다. 따라서 n t =m이 된다. 메 타모델의 정확한 평가를 위해서는 표본점이 아닌 새로운 설계점 n t 를 시험점으로 하여 생성된 메타모델의 평균제 곱오차(mean square error)를 구하는 것이다. 그러나 이 경우 새로운 설계점에 대한 구조해석을 필요로 하고 이 것은 메타모델을 사용하는 취지에 역행하는 것이다. 반면에 식 (10)을 이용하게 되면 추가적인 설계점이 필요 없어 기존의 표본점을 갖고 메타모델을 평가 할 수 있다. 그러나 이 역시 표본점 수 m개 만큼 메타모델을 생 성해야 하므로 매우 번거로운 과정을 유발한다. 이의 단 점을 극복하기 위해 k-평균 클러스터(k-means cluster) 의 개념을 도입한다. 이 개념을 Fig. 1에 표시하였다. 본 연구에서는 Forgy의 알고리듬을 이용하였다. k-평균 클 러스터를 이용하면 메타모델의 생성횟수를 m개에서 k개 로 줄일 수 있다. 따라서 식 (10)의 CV 검증지수는 다음 과 같이 변형된다. k GMSE = ∑ CV k i = 1 where CV k = n 1 k ∑ i n = k 1 ( y i − y ^ _ k ) 2 (11) 여기서 n k 는 k번째 클러스터에 포함된 표본점의 개수, ^ y _ k 는 k번째 클러스터에 포함된 표본점을 제외한 표본 점 (m-n k )개를 갖고 생성된 메타모델이다. 식 (11)을 이 용하면 표본점 이외의 추가 설계점 없이 평균제곱오차를 효율적으로 계산할 수 있는 장점이 있다.
혼합모델을 위한 2개의 가중치는 다음과 같이 계산된다.
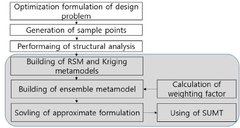
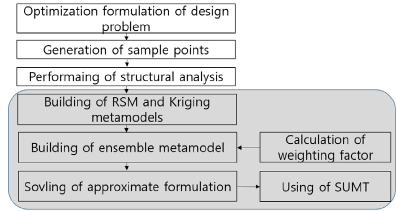
여기서 식 (9)의 다중목적함수를 위한 w R , w k 는 각각 반 응표면모델과 크리깅모델의 가중치이다. 또한 GMSE R 과 GMSE K 는 반응표면모델과 크리깅모델에 대한 식 (11)의 GMSE이다. 3.3 혼합메타모델을 이용한 최적설계과정 제안 본 연구에서는 구조최적설계를 위한 설계과정을 Fig. 2와 같이 제안한다.
[Fig. 2] Suggested design process 먼저 구조최적설계를 위한 목적함수, 제한조건함수를 결정한다. 그 다음 메타모델을 구성하기 위한 표본점을 결정한다. 표본점을 결정하는 방법으로는 D-optimal 방 법, 중심합성법, 라틴하이퍼큐브방법, 직교배열표, 전조 합실시법 등이 있다. 본 연구에서는 Matlab에 내장되어 있는 라틴하이퍼큐브의 표본점 생성 명령어인 lhsdesign 을 이용하였다. 그 다음, 표본점에 대응하는 구조해석을 실시한다. 구 조해석 후 목적함수 및 제한조건함수에 포함되어 있는 반응치들을 추출한다. 이 반응치를 갖고 반응표면모델과 크리깅모델을 생성한다. 각 모델을 생성하기 전에 k-평 균 클러스터를 설정하여 각 모델에 대한 GMSE를 저장 한다. 이 값을 기초로 각 모델의 가중치를 계산한다. 또는 가중치를 설계자가 직관적으로 부여할 수 있도록 선택사 항으로 취급하였다.
최적설계를 위한 정식화를 근사화시킨다. 마지막 단계로 서, 근사화된 최적화문제를 SUMT 기법으로 해결한다. 본 연구에서는 설계과정을 요약한 Fig. 2에서 음영으로 표시된 부분을 자동화시켰다.
4. 2부재 및 아우터타이로드의 구조설계
본 연구에서 제시한 설계과정을 이부재 설계문제[1, 14]와 승용차용 아우터타이로드의 형상설계 문제[15, 16] 에 적용하였다.
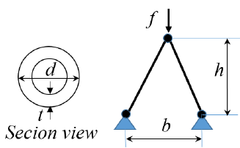
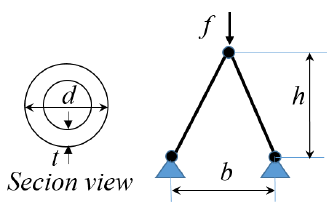
4.1 이부재(two-bar) 설계문제 15 31.7 439.1 433.3 595.4 337.4 16 71.6 629.4 1101.1 207.5 1352.3 이부재의 형상은 Fig. 3과 같고 탄성계수 E=205GPa, 17 21.8 892.9 400.1 571.0 88.7 18 66.5 345.8 862.7 343.0 1639.8 수직하중 f=150kN, t=2mm, b=750mm이다. 설계변수는 19 38.8 824.3 678.9 332.9 306.2 튜브의 지름 d와 구조물의 높이 h이다. 구조물의 강도 기 20 36.1 250.7 448.4 834.4 527.0 준을 만족시키면서 체적을 최소화하기 위한 최적설계 정 식화는 다음과 같이 표현된다. [Table 2] Parameter values for metamodels (two-bar)
[Fig. 3] Two-bar design problem Minimize V Subject to S ≤ S max S ≤ S crit 20 mm ≤ d ≤ 80 mm , 200 mm ≤ H ≤ 1000 mm , t = 2 . 5 mm V = 2 π dt b 2 + h 2 , S = f 2 b π 2 dth + h 2 , S crit = 8 ( π b 2 2 Ed + h 2 2 ) , (13) 여기서 V는 체적, S는 수직응력, S crit 는 임계좌굴응력을 표시하며 S max =400MPa이다. 먼저 표본점을 라틴하이퍼큐브 방법으로 생성한 다음, 구조설계를 위한 반응치 V, S, S crit 를 Table 1과 같이 구 하였다. 본 예제의 결과 검토를 위해 500개의 시험 점을
[Table 1] Design of experiments for two-bar design d h V S Scrit (mm) (mm) (mm3) (MPa) (MPa) 1 55.5 582.6 827.4 280.7 862.7 2 58.7 498.0 830.4 294.0 1076.1 3 70.1 733.1 1154.1 195.0 1128.3 4 34.4 955.1 655.3 353.5 202.4 5 59.6 854.8 1065.3 213.0 695.5 6 77.7 550.9 1135.4 207.7 1761.9 7 26.2 681.4 416.6 542.6 168.7 8 64.7 447.0 886.7 288.5 1387.1 9 41.8 376.5 550.4 509.8 626.2 10 46.4 643.0 720.4 316.0 558.5 11 51.8 298.2 656.2 499.3 1040.0 12 25.5 992.1 498.7 469.0 106.5 13 48.7 761.2 817.8 275.2 525.7 14 76.0 224.5 935.2 437.9 2386.3
Parameter values for metamodels (two-bar)
RSM Kriging No. m of Res. (i=1∼10) β i b, θ 1 , θ 2 V -0.203, -0.018, 0.280, 0.012, 0.974, 0.219, -0.088 .064, 0.321, 0.006, 0.753,0.180 0.913, 2.052, -4.142, -4.490, S -1.495, 4.141, -2.082,-1.520, 3.998, 5.168, 1.347, 2.084,1.875 -2.138 0.031, 0.434 ,0.011, 20 S crit -0.435, -0.427, 0.100 0.152, 0.722, -0.151, -0.052, 1.532, 0.146, 0.504 V: 1.1 V: 1.3 RMSE S: 33.7 S: 30.1 S crit : 8.0 S crit : 3.8 Optimum value) (true Sc=398.19(398.7) V=564.1(563.8) S=411.23(398.7) d=37.75, h=585.25, Sc=400.9(400.2) V=570.9(570.8) S=405.2(399.9) d=38.04, h=591.9, -0.076, 0.614, 0.025, V -0.007, 0.229, 0.003, 0.168, -0.001, 0.168, 0.690, 0.611, 0.396 -0.074 1.972, -3.509, -3.569, S -0.513, 2.028, 3.425, -0.743,-1.416, 3.847, 3.112, 1.436, 2.324 -1.565 30 S crit -0.524, -0.389, 0.144 0.005, 0.573, 0.516, 0.195, -0.234, 0.070, 0.043, 6.803, 0.042, 0.720 V: 0.6 V: 0.2 RMSE S: 26.3 S: 20.0 S crit : 6.2 S crit : 0.2 Optimum value) (true S=398.01(404.82) V=570.4(570.4) d=37.89 h=596.6, S=400.0(399.6) d=36.72, V=569.7(569.7) h=642.78
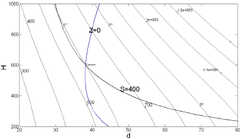
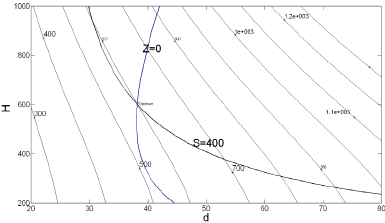
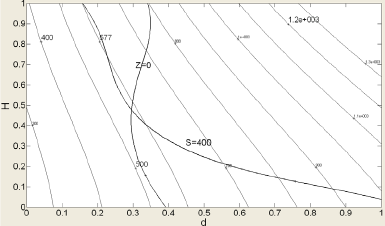
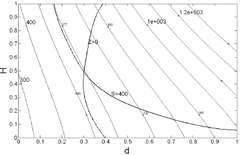
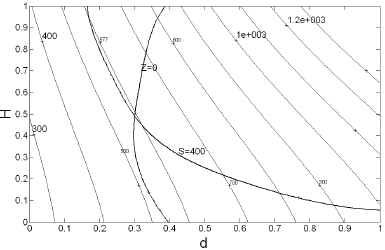
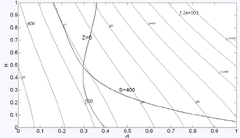
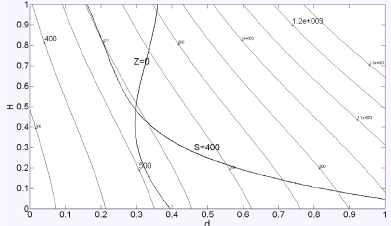
설정하였고 이에 대한 평균제곱오차 MSE를 계산하였 다. 먼저 각 반응치 V, S, S crit 의 반응표면모델과 크리깅 모델을 각각 생성하였으며 이를 Table 2에 표시하였다. 식 (5) 및 식 (7)에 포함된 반응표면모델과 크리깅모델의 파라미터 값을 Table 2에 정리한 것이다. 표본점 m=20일 때, RMSE 값을 보면 반응표면모델이 반응치 V에 대해 우수하고, 크리깅모델이 S, S crit 에 대해 우수한 결과를 보 이고 있다. 반면에 m=30일 때는 모든 반응치에 대해 크 리깅 모델이 우수함을 보이고 있다. [Table 3] Weighting factor and RMSE of ensemble model Cluster:3 Ccluster:6 Cluster:9 Res. RSM KRIG RSM KRIG RSM KRIG (W R ) (W K ) (W R ) (W K ) (W R ) (W K ) V 0.282 0.718 0.304 0.696 0.365 0.635 S 0.424 0.576 0.522 0.478 0.706 0.294 S crit 0.478 0.522 0.383 0.617 0.241 0.759 V: 0.7 V: 0.8 V: 0.6 RM S: 17.3 S: 17.2 S: 21.7 SE S crit : 2.9 S crit : 2.1 S crit : 2.1 클러스터의 개수를 각각 3개, 6개, 9개로 설정하였을 때 혼합메탈모델을 위한 가중치의 값을 Table 3에 정리 하였다. 클러스터 개수를 6개로 설정하였을 때 가장 신뢰 도 있는 혼합메타모델이 생성이 되었다. 또한 Table 2의 반응표면과 크리깅의 단일메타모델의 RMSE와 비교 시, Table 3의 모든 혼합메타모델의 신뢰도가 높게 평가되고 있다. 반면에 m=20개와 클러스터 6개로 구해진 혼합메타 모델과 m=30개로 구해진 단일메타모델을 비교하면, 단 일 반응메타모델보다는 우수하지만 단일 크리깅 메타모 델보다는 열세임을 알 수 있다. 식 (13)의 초기 최적화문제를 Fig. 4(a)에 도식적으로 표시하였다. 여기서 변수 Z=S/S crit 를 의미한다. 곡선 S와 Z의 교차점이 최적해이며 그 값은 d=38.20mm, h=600.3mm이 고, 그 때의 반응치는 각각 V=576.5mm 3 , S=400.0MPa, S crit =400MPa이다. 다음의 Fig. 4(b), (c)는 각각 반응표 면모델과 크리깅으로 근사화시킨 최적화 문제이다. Fig. 4(d)는 본 연구에서 제안한 혼합메타모델로 근사화시킨 최적화문제이다. 표본점의 개수 m=30일 경우, Table 2에 표시한 것과 같이 크리깅모델의 신뢰도가 높이 평가되고 있다. 이럴 경우 식 (9)로 정의되는 혼합메탈모델의 RMSE가 단일
(a) Original optimization problem(b) Approximation model using RSM(c) Approximation model using Kriging
(d) Approximation model using ensemble model (k=6) [Fig. 4] Graphical representation of optimization problem defined in Eq. (13)
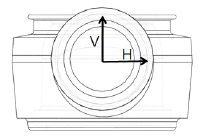
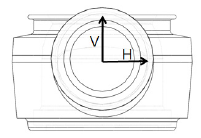
4.2 아우터타이로드(two-bar) 설계문제[15] 아우터타이로드는 조향계 부품으로서 초기에 강으로 설계되었으나 이를 알루미늄으로 변경하고 형상최적설 계를 통해 경량화 시키려는 부품이다. 이 부품은 이미 참 고문헌 [15]에서 반응표면모델과 크리깅모델의 단일메타 모델을 가지고 최적설계를 제시한 바 있다. 아우터타이 [Fig. 7] Definition of design variable 로드의 초기설계를 Fig. 5에 표시하였으며, 초기모델에 대한 좌굴해석 결과를 Fig. 6에 표시하였다. 본 연구에서 [Table 4] Design of experiments for OTR design 는 혼합메타모델에 의한 최적해를 산출하고자 한다. Exp. V H Weight R 구조최적설계를 위한 정식화는 다음과 같이 표현된다. No. (mm) (mm) (kg) (kN)
Minimize Weight Subject to R ≥ R max 10 . 35 mm ≤ V ≤ 12 . 65 mm , 10 . 35 mm ≤ H ≤ 12 . 65 mm (14) 여기서 R은 좌굴하중이며 R max 는 허용좌굴하중을 의미 하고 설계변수 V, H는 Fig. 7과 같이 정의된다. 식 (14)의 목적함수에서 Weight와 제한조건함수에서 좌굴하중 R을 혼합메타모델로 대치하여 최적해를 산출 하고자 한다. 이를 위해 표본점은 Table 4와 같이 전조합 실시법을 이용하여 결정되었다. 아우터타이로드의 중량 및 좌굴하중에 대한 반응표면모델과 크리깅모델에 대한 단일메타모델의 파라미터 값을 Table 5에 정리하였다. 혼합메타모델 생성 시, 클러스터 개수는 5로 설정하였다. 반응표면모델의 오차가 참고문헌 [15]와 비교하여 작은 이유는 본 연구에서 다항식을 3차식으로 가정했기 때문이다. 혼합메타모델을 위한 가중치는 중량에 대하여 W R =0.603, W K =0.397이고 좌굴하중에 대하여 W R =0.712, W K =0.288 이 산출되었다. 식 (14)의 최적화문제에서 중량 및 좌굴 하중을 혼합메타모델로 대치한 결과, 최적해는 V=11.32mm, 10.35mm가 산출되었고 이 값은 Table 5에서 얻은 결과 와 거의 일치하고 있다.
[Fig. 5] Initial design of the OTR
Definition of design variable
Design of experiments for OTR design
1 10.35 10.35 310.88 27.769 2 10.35 10.925 325.65 29.318 3 10.35 11.5 340.39 30.829 4 10.35 12.075 355.19 32.359 5 10.35 12.65 366.04 33.284 6 10.925 10.35 325.65 32.062 7 10.925 10.925 341.15 33.706 8 10.925 11.5 356.75 35.427 9 10.925 12.075 372.28 37.034 10 10.925 12.65 383.78 38.142 11 11.5 10.35 340.39 36.228 12 11.5 10.925 356.75 38.326 13 11.5 11.5 373.17 40.074 14 11.5 12.075 389.42 41.735 15 11.5 12.65 401.54 42.92 16 12.075 10.35 355.13 40.814 17 12.075 10.925 372.25 42.894 18 12.075 11.5 389.42 44.678 19 12.075 12.075 406.57 46.387 20 12.075 12.65 419.28 47.816 21 12.65 10.35 369.79 45.316 22 12.65 10.925 387.77 47.112 23 12.65 11.5 401.54 49.396 24 12.65 12.075 419.28 51.186 25 12.65 12.65 441.75 53.06 [Table 5] Parameter values for metamodels (OTR) RSM Kriging Reponse β i b, θ 1 , θ 2 (i=1∼10) -0.006, 0.473, 0.501, 0.403 Weight -0.073, 0.017, -0.011, 3.503, 1.402 0.036, 0.142, -0.033, -0.06 -0.003, 0.686,0.255, 0.040, 0.004, 0.035, 0.456 R 0.012, 0.028, 0.003, 1.588, 2.550 -0.069 Weight: 0.142 Weight: 0.216 GMSE R: 0.081 R: 0.201 Optimum V=11.32, H=10.35, V=11.33, H=10.35, (true Weight=336.1(335.7) Weight=336.4(336.1) value) R=35.0(35.1) R=35.0(35.2) Weight WR: 0.603 WK: 0.397
5. 결 론
본 연구에서는 혼합메타모델을 구성하여 구조최적설 계에 적용하는 절차를 제시하였으며 다음과 같은 결론을 얻었다. (1) 자유도가 많은 대형 구조설계 문제, 동적해석이 포 함된 설계문제, 복잡한 형상설계변수가 정의되어 야 하는 형상최적화 문제, 강건설계 문제 등에 메 타모델기법을 이용한 최적설계 적용 시, 반응표면 모델이나 크리깅모델의 신뢰도가 만족스럽지 못 할 때 혼합메타모델을 이용하면 보다 향상된 메타 모델을 구성할 수 있다. (2) 표본점 수를 많이 생성 할 수 있는 설계 문제에서 는 경험적으로 크리깅 메타모델이 반응표면 모델 보다 RMSE의 값이 작게 산출된다. 따라서 크리 깅의 단일 메타모델을 구성하여 최적해를 구하는 것을 추천한다. 단, 국부적으로 크리깅모델은 오버 피팅 될 수 있는 단점이 있다. (3) 본 연구에서는 제안한 설계방법을 이부재 설계문 제와 아우터타이로드 설계에 적용하여 이에 대한 효용성을 검증하였다. 이부재 설계문제에서 클러 스터 6개인 혼합모델은 반응표면모델에 비교하여 V, S, S crit 의 GMSE 값이 각각 0.3, 16.5, 5.9 만큼의 작은 값을 보이고 있다. 크리깅모델에 비교하여 V, S, S crit 의 GMSE 값은 각각 0.5, 12.9, 1.7 만큼의 작 은 값을 보이고 있다. 반면에 이우터타이로드의 경 우에는 반응표면과 크리깅에 의한 최적해가 매우 근접해 있어 혼합모델에 의한 값 역시 큰 차이를 보이고 있지 않다.
References
- [1] K.H. Lee, “A Robust Structural Design Method Using the Kriging Model to Define the Probability of Design Success,” Journal of Mechanical Engineering Science, Vol. 224, No. 2, pp.379-388, 2010. DOI: http://dx.doi.org/10.1243/09544062JMES1736 [DOI]
- [2] G.Y. Kim, S.H. Han, S.H. K.H., Lee, "Structural Optimization of a Knuckle with Consideration of Stiffness and Durability Requirements," The Scientific World Journal, Vol. 2014, Article ID 763692, 2014. optimization of an Upper Control Arm, Considering the Strength,” Journal of Automobile Engineering, Vol. 223, No. 6, pp. 727-735, 2009. DOI: http://dx.doi.org/10.1243/09544070JAUTO1090 [DOI]
- [4] ANSYS, http://www.ansys.com. [DOI]
- [5] LS-OPT, http://www.lstc.com/products/ls-opt. [6] PAM-OPT, http://www.esi.com.au/Software/PAM-OPT.html. [possible DOI] [alternative DOI]
- [7] PiANO, http://pidotech.com. [DOI]
- [8] VisualDOC, https://www.vrand.com. [DOI]
- [9] S IG H T , h ttp://w w w .3d s.com /produ cts- serv ices/sim u lia/produ cts/isig h t- sim u lia- execution-engine. [possible DOI] [alternative DOI]
- [10] L.E. Zerpa, N.V. Queipo, S. Pintos, J.L. Salager, "An Optimization M ethodology of Alkaline-Surfactant-Polymer Flooding Processes Using Field Scale Numerical Simulation and Multiple Surrogates," Journal of Petroleum Science and Engineering, Vol. 47, No. 3-4, pp. 197-208, 2005. DOI: http://dx.doi.org/10.1016/j.petrol.2005.03.002 [DOI]
- [11] E. Acar, M Rais-Rohani, "Ensemble of Metalmodels with Optimized Weighting Factors," Structural Multidisciplinary Optimization, Vol. 37, pp. 279-294, 2009. DOI: http://dx.doi.org/10.1007/s00158-008-0230-y [DOI]
- [12] FAC Viana, R.T. Haftka, V. Steffen, "Multiple Surrogates: How Cross-Validation Errors Can Help Us to Obtain the Best Predictor," Structural Multidisciplinary Optimization, Vol. 39, Vol. 4, pp. 279-294, 2009 [DOI]
- [13] H. Yin, G. Wen, H. Fang, Q. Qing, X. Kong, J. Xiao, Z. Liu, "Multiobjective Crashworthiness Optimization Design of Functionally Graded Foam-Filled Tapered Tube Based on Dynamic Ensemble Metamodel," Materials & Design, Vol. 55, pp.747-757, 2014. DOI: http://dx.doi.org/10.1016/j.matdes.2013.10.054 [DOI]
- [14] K.H. Lee, D.H. Kang, “A Robust Optimization Using the Statistics Based on Kriging Metamodel,” J. of Mechanical Science and Technology, Vol. 20, No. 8, pp. 1169-1182, 2006. [DOI]
- [15] Y.J., Kim, G.J., Ahn, K.H. Lee, Y.C. Park, "Structural Optimization of an Outer Tie Rod Using RSM and Kriging," Journal of KAIS, Vol. 16, No. 1, pp. 27-34, 2015. DOI: http://dx.doi.org/10.5762/KAIS.2015.16.1.27 [DOI]
- [16] J.K. Kim, Y.J. Kim, W.H. Yang, Y.C. Park, K.H. Lee, “Structural Design of an Outer Tie Rod for a Passenger Car,” International Journal of Automotive Technology, Vol. 12, No. 3, pp. 375-381, 2011. DOI: http://dx.doi.org/10.1007/s12239-011-0044-6 [DOI]
- [17] G.E.P. Box, K.B., Wilson, "On the Experimental Attainment of Optimum Conditions," Journal of the Royal Statistical Society, Series B, Vol. 13, pp.1-45, 1950. 이 권 희 (Kwon-Hee Lee) [정회원] • 1991년 2월 : 한양대학교 공과대학 기계설계학과 (공학석사) • 1997년 2월 : 한양대학교 공과대학 기계설계학과 (공학박사) • 1994년 6월 ∼ 1999년 6월 : 대우 자동차 선임연구원 • 2002년 3월 ∼ 현재 : 동아대학교 기계공학과 교수 [DOI]
- <관심분야> 기계설계, 최적설계 [possible DOI] [alternative DOI]
- 김 남 희 (Nam-Hee Kim) [준회원] •2014년 2월 : 동아대학교 기계공학 과 (공학사) •2015년 3월 ∼ 현재 : 동아대학교 기계공학과 석사 재학 <관심분야> 구조해석, 차량부품해석 [DOI]